개요
분석 및 통계에 널리 사용되는 R은 다음과 같은 특징을 가진다.
- 수리통계에 특화된 특정 도메인 언어(DSL: Domain-specific Language)
- 함수형 언어
- 객체지향형 언어
- 인터프리터형 언어
특히 인터프리터형 언어로서의 R은 대화형으로 동작하기 때문에 사용이 매우 쉽다. 또한 함수형 언어이므로 모든 명령은 함수로 동작할 뿐 아니라 함수 그 자체를 함수의 인자(argument)로 사용할 수 있어서 다른 프로그래밍 언어보다 훨씬 간결하다.
그러나 간단한 명령어만으로도 산출물이 손쉽게 나오다 보니 정확한 의미와 배경을 이해하지 않고서는 결과의 해석에 애를 먹거나 심지어 잘못된 결과를 가지고 작업을 마치는 경우조차 발생하게 된다. 이를 극복하기 위해서는 무엇보다 R의 기본구문과 수리 및 통계학적 이론을 다져야 한다.
R에서의 확률분포
확률이란 특정한 사건이 일어날 가능성을 말하며, A라는 특정 사건이 일어날 확률을 P(A)로 표시할 때 다음과 같이 계산할 수 있다.

그리고 이러한 확률은 두 가지의 기본 속성을 갖고 있다.

확률실험에서 가능한 모든 결과의 집합을 표본공간(sample space)이라 한다. 이때 표본공간상에서 확률실험을 반복하면 확률변수의 분포를 얻을 수 있는데, 그 성격에 따라 이산확률변수와 연속확률변수로 나누어 볼 수 있다.
- 이산확률분포는 확률변수가 이산(discrete) 변량인 경우로서 확률질량함수(probability mass function: pmf)로 표현된다. 이산확률분포의 대표적인 것은 이항분포와 포아송 (Poisson) 분포다.
- 연속확률분포는 확률변수가 연속(continuous) 변량인 경우로서 확률밀도함수(probability density function: pdf)로 표현되며 대표적인 것은 정규분포와 t-분포다.
한편 모집단은 연구대상이 되는 사람 또는 사물의 전체집합이다. 모집단분포(population distribution)란 연구대상이 되는 전체의 속성을 나타내는 분포라 할 수 있는데 다음의 지표로 표현된다.

그러나 모집단은 방대하므로 그 속성을 올바르게 파악하기란 쉽지 않아서 모집단을 대표할 수 있는 표본을 추출해 그 속성으로 모집단의 속성을 추측하는 경우가 일반적이다. 표본분포(sample distribution)란 모집단을 대표하도록 추출된 것으로서 그 표본분포의 특성을 표본통계량 또는 추정치(estimates)라고 부르고 다음의 지표로 표현한다.

그런데 이와 구분되는 것이 표본추출분포 또는 표집분포(sampling distribution)다. 표집분포는 크기가 n인 표본을 무한 반복추출 한 후 이들의 평균을 가지고 그린 것을 말한다. 여기서 유의할 것은 모집단분포와 표본분포가 실제 현실에서 얻을 수 있는 분포인 반면, 표집분포는 일정한 가정을 전제로 해 이론적으로만 그려질 수 있다는 점이다. 그러나 모집단을 대표할 수 있는 완벽한 표본추출은 실제로 불가능하므로 평균과 표집분포에서의 평균 사이에 오차가 발생하는데 이를 표집오차(sampling error)라고 한다. 표집분포의 평균과 표준오차의 추정에는 복잡한 수학적 전개가 요구되지만, 핵심적인 역할을 하는 개념이 중심극한정리(central limit theorem)다.
중심극한정리
중심극한정리는 대수(大數)의 법칙(Law of Large Numbers)으로도 불리며, 다음과 같이 정리될 수 있다.

- ① 표본의 크기가 충분히 큰 경우(n≥ 30 ) 모집단의 분포가 어떠한 형태이든 상관없이 정규본포를 이룬다.
- ② 표본의 크기가 크지 않은 경우(n< 30 )에도 모집단이 정규분포인 경우에는 표본평균 역시 표본의 크기에 상관 없이 정규분포를 이룬다.
그리고 이들 경우에 표본의 평균과 모집단의 평균이 같다는 것이 수학적으로 증명되었다.
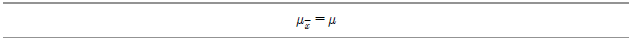
한편 표본평균의 표준편차(이를 평균의 표준편차: standard error of the mean라고 부른다)는 모집단의 표준편차를 표본의 수의 제곱근으로 나눈 것과 같다.
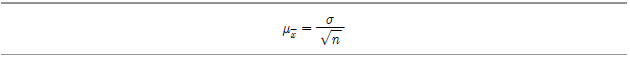
[그림 Ⅳ-2-1]에서는 4개의 모집단이 서로 다른 분포를 가짐에도 표본의 수가 증가함에 따라 각각 정규분포에서 유사한 모습을 띄게 되는 것을 보여주고 있다.
![[그림 Ⅳ-2-1] 표본 크기의 증가에 따른 표본평균분포곡선의 변화 모습](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_08.png)
[그림 Ⅳ-2-1] 표본 크기의 증가에 따른 표본평균분포곡선의 변화 모습
뒤에서 실제로 이러한 변화가 일어나는지를 R 명령어를 통해 실험해 보겠다.
확률분포와 관련된 R 명령어
이제 R에서 확률 분포를 이용하기 위한 관련 명령어를 살펴보자. 다만 R에서는 많은 확률분포를 이용할 수 있는데 여기서는 지면의 한계로 인해 주요한 몇 가지만 살펴보기로 한다. R에서 제공되는 전체 확률분포를 알고자 한다면 다음과 같이 도움말을 요청하면 된다.

모든 확률분포에 대해 다음과 같은 4가지의 함수 대표어(function family)가 적용된다. 이들 명령어는 접두어처럼 개별 분포함수의 앞에 붙이는 방식(d,p,q,r+함수명의 형식)으로 기능을 지정한다.

- 정규분포
- 정규분포와 관련된 함수에는 앞의 규칙에 따라 4가지가 있으며 그 주요내용은 다음과 같다.
![[함수 표준형] dnorm(x, mean = 0, sd = 1. log = FALSE) / pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE) / qnorm(p, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE) / rnorm(n, mean = 0, sd = 1), [옵션 파라미터] mean = 평균, sd = 표준편차, lower.tail = 좌측단측 여부, log = 확률이 log값으로 제시되는지 여부](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_11.png)
이들 각각에 적용되는 많은 옵션에 대해서는 다음 명령을 통해 그 목록을 받아볼 수 있다.

우선 dnorm 함수를 살펴 본다. 하나의 값을 제시하면 dnorm 함수는 여기에 대응되는 확률분포값(확률분포곡선 상의 높이값)을 반환한다. 평균 및 표준분포 등의 값을 제시하면 이에 기반한 값이 반환되지만, 별다른 옵션이 제시되지 않으면 평균이 0이고 표준편차가 1인 표준정규분포를 전제로 해 해당 값을 반환하게 된다.
![> dnorm(0) [1] 0.3989423 > dnorm(0)*sqrt(2*pi) [1] 1 >dnorm(0, mean=4) [1] 0.0001338302 > dnorm(0, mean=4, sd=10) [1] 0.03682701 >v <- c(0,1,2) > dnorm(v) [1] 0.39894228 0.24197072 0.05399097 > x < - seq(-20,20,by=.1) > y <-dnorm(x) > plot(x,y) > y < - dnorm(x, mean=2.5, sd = 0.1) >plot(x,y)](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_13.png)
두 번째 함수로는 pnorm이 있다. 이는 특정 숫자 또는 리스트 데이터를 제시하면 그 숫자 이하에 해당되는 정규분포상의 random number를 반환한다.
![> pnorm(0) [1] 0.5 > pnorm(1) [1] 0.8413447 > pnorm(0, mean=2) [1] 0.02275013 > pnorm(0, mean=2, sd=3) [1] 0.2524925 > v <- c(0,1,2) > pnorm(v) [1] 0.5000000 0.8413447 0.9772499 > x <- seq(-20, 20, by=.1) > y <-pnorm(x) >plot(x,y) > y <- pnorm(x, mean=3, sd=4) >plot(x,y)](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_14.png)
만약 제시된 숫자 이상의 확률값을 원한다면 lower.tail 옵션에서 이를 지정할 수 있다.
![> pnorm(0,lower.tail=FALSE) [1] 0.5 > pnorm(1, lower.tail=FALSE) [1] 0.1586553 > pnorm(0, mean=2, lower.tail=FALSE) [1] 0.9772499](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_15.png)
다음으로 qnorm 함수가 있는데 이는 pnorm 함수와는 반대(inverse)라 할 수 있다. 즉, qnorm 에서 사용자가 확률을 제시하면 이 확률의 누적값에 대응되는 숫자를 반환한다. 예를 들어 평균=0, 표준편차=1의 정규분포 상에서 확률값을 제시하면 여기에 대응되는 Z-score가 반환된다.
![>qnorm(0.5) [1] 0 > qnorm(0.5, mean=1) [1] 1 >qnorm(0.5, mean=1, sd=2) [1] 1 >qnorm(0.5, mean=2, sd=2) [1] 2 >qnorm(0.25, mean=2, sd=2) [1] 0.65101205 >qnorm(0.333) [1] -0.4316442 > qnorm(0.333, sd=3) [1] -1.294933 > qnorm(0.75, mean=5, sd=2) [1] 6.34898 > v = c(0.1, 0.3, 0.75) >qnorm(v) [1] -1.2815516 -0.5244005 0.6744898 > x <-seq(0,1,by=.05) > y <-qnorm(x) >plot(x,y) > y <-qnorm(x, mean=3, sd=2) >plot(x,y) > y <-qnorm(x, mean=3, sd=0.1) >plot(x,y)](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_16.png)
마지막으로 rnorm 함수는 정규분포에 의거한 난수(random number)를 생성한다. 이때 몇 개의 난수를 생성할 것인지를 제시하는데 필요하다면 평균값과 표준편차 값도 아울러 제시할 수 있다.
![> rnorm(4) [1] 1.2387271 -0.2323259 -1.2003081 -1.6718483 > rnorm(4, mean=3) [1] 2.633080 3.617486 2.038861 2.601933 > rnorm(4, mean=3, sd=3) [1] 4.580556 2.974903 4.756097 6.395894 > rnorm(4, mean=3, sd=3) [1] 3.000852 3.714180 10.032021 3.295667 > y <-rnorm(200) >hist(y) > y <-rnorm(200, mean=-2) >hist(y) >y <-rnorm(200, mean=-2, sd=4) >hist(y) >qqnorm(y) >qqline(y)](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_17.png)
- t-분포
- t-분포와 관련된 값을 생성할 수 있는 함수 역시 앞서의 규칙에 따라 4가지가 존재한다.
![[함수표준형] dt(x, df=a) / pt(q, df=a) / qt(p, df=a) / rt(n, df=a), [옵션 파라미터] df = 자유도](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_18.png)
이들 명령어는 정규분포의 그것과 거의 동일한 방식으로 이용할 수 있는데, 몇 가지 차이가 있다면 우선 평균=0, 표준편차=1을 전제로 한 값으로 계산된다는 점이다. 따라서 실제 사용 시에는 별도의 변형작업이 필요할 수 있음을 감안해야 한다. 아울러 자유도(degree of freedom)의 지정 역시 유의해야 한다. 이러한 사항을 제외한다면 명령어에 대한 이름규칙도 동일해서 dt, pt, qt and rt 등의 이름을 사용하게 된다.
우선 t-분포의 높이를 반환하는 dt 함수를 살펴 본다.

다음으로 t-분포에 대한 누적확률밀도함수를 살펴 본다.
![> pt(-3,df=10) [1] 0.006671828 > pt(3, df=10) [1] 0.9933282 > 1-pt(3, df=10) [1] 0.006671828 >pt(3, df=30) [1] 0.996462 > x = c(-3, -4, -2, -1) >pt((mean(x)-2)/sd(x), df=40) [1] 0.000603064](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_20.png)
t-분포에서의 누적확률분포 역함수(inverse cumulative probability distribution function)는 다음과 같다.
![> qt(0.05,df=10) [1] -1.812461 > qt(0.95, df=10) [1] 1.812461 > qt(0.05, df=20) [1] -1.724718 >qt(0.95, df=20) [1] 1.724718 > v <- c(0.005, .025, .05) >qt(v,df=253) [1] -2.595401 -1.969385 -1.650899 >qt(v,df=25) [1] -2.787436 -2.059539 -1.708141](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_21.png)
끝으로 t-분포에 의거해 난수를 발생시키는 경우 그 방법은 다음과 같다.
![> rt(3, df=10) [1] 0.9440930 2.1734365 0.6785262 > rt(3, df=20) [1] 0.1043300 -1.4682198 0.0715013 > rt(3, df=20) [1] 0.8023832 -0.4759780 -1.05461255](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_22.png)
- 이항분포
- 이항분포에 의거해 값을 생성시키는 함수 역시 4가지가 있다. 이 명령어들도 정규분포의 그것과 거의 동일하지만, 함수에 전달되는 파라미터에는 두 가지가 추가된다. 즉, 단일 실행 시의 성공 확률과 전체 시행횟수가 그 것이다. 그 외에는 사용법이 거의 동일하며 함수의 이름 역시 동일한 규칙에 의거해 dbinom, pbinom, qbinom, rbinom으로 지정된다.
![[함수표준형] dbinom(x, size, prob, log = FALSE) / pbinom(q, size, prob, lower.tail = TRUE, log.p = FALSE) / qbinom(p, size, prob, lower.tail = TRUE, log.p = FALSE) / rbinom(n, size, prob) [옵션파라미터] 앞서의 정규분포 관련 함수에서와 동일하다.](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_23.png)
우선 이항분포의 높이를 반환하는 dbinom 함수를 살펴본다

다음으로 이항분포에서의 누적확률함수를 살펴 본다.
![> pbinom(24,50,0.5) [1] 0.4438624 > pbinom(25, 50m 0.5) [1] 0.5561376 > pbinom(25, 51, 0.5) [1] 0.5 > pbinom(26, 51, 0.5) [1] 0.610116 > pbinom(25, 50, 0.5) [1] 0.5561376 > pbinom(25, 50, 0.25) [1] 0.999962 > pbinom(25, 500, 0.25) [1] 4.955658e-33](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_25.png)
다음으로 이항분포에서의 누적확률분포 역함수(inverse cumulative probability distribution function)를 살펴 본다.
![> qbinom(0.5, 51, 1/2) [1] 25 > qbinom(0.25, 51, 1/2) [1] 23 > pbinom(23, 51, 1/2) [1] 0.2879247 > pbinom(22. 51, 1/2) [1] 0.200531](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_26.png)
마지막으로 이항분포에 의거해 난수를 발생시키는 경우를 살펴 본다.
![> rbinom(5,100,.2) [1] 30 23 21 19 18 > rbinom(5, 100, .7) [1] 66 66 58 68 63](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_27.png)
- 카이제곱
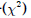 ?분포
?분포
- 마찬가지로 카이제곱분포와 관련된 함수도 다음과 같은 네 가지가 있다.
![[함수표준형] dchisq(x, df, ncp=0, log = FALSE) / pchisq(q, df, ncp = 0, lower.tail = TRUE, log.p = FALSE) / qchisq(p, df, ncp = 0, lower.tail = TRUE, log.p = FALSE) / rchisq(n, df, ncp = 0)](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_29.png)
[옵션파라미터]는 앞서 정규분포에서와 같으며 정규분포와 동일한 방식으로 이용된다. 다만 정규분포를 전제로 계산되므로 평균값을 따로 지정하지 않아도 된다는 것과 자유도를 지정해야 한다는 점에 차이가 있다.
카이제곱분포의 높이를 반환하는 dchisq 함수를 살펴본다

다음으로 누적확률밀도함수를 살펴 본다.
![> pchisq(2,df=10) [1] 0.003659847 > pchisq(3, df=10) [1] 0.01857594 > 1-pchisq(3, df=10) [1] 0.981424 > pchisq(3, df=20) [1] 4.097501e-06 > x = c (2, 4, 5, 6) > pchisq(x, df=20) [1] 1.114255e-07 4.649808e-05 2.773521e-04 1.102488e-03](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_31.png)
다음으로 누적확률분포의 역함수를 살펴 본다.
![>qchisq(0.05, df=10) [1] 3.940299 > qchisq(0.95, df=10) [1] 18.30704 >qchisq(0.05, df=20) [1] 10.85081 > qchisq(0.95, df=20) [1] 31.41043 > v <-c(0.005, .025, .05) > qchisq(v, df=253) [1] 198.8161 210.8355 217.1713 > qchisq(v, df=25) [1] 10.51965 13.11972 14.61141](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_32.png)
마지막으로 카이제곱 분포에 의거한 난수 생성의 모습을 살펴본다.
![> rchisq(3,df=10) [1] 16.80075 20.28412 12.39099 > rchisq(3, df=20) [1] 17.838878 8.591936 17.486372 > rchisq(3, df=20) [1] 11.19279 23.86907 24.81251](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_33.png)
이상의 R에서의 확률분포를 정리하면 다음과 같다.
| 분포 |
확률함수 |
누적확률 |
분위 |
난수 |
| 정규분포 |
dnorm() |
pnorm() |
qnorm() |
rnorm() |
| 카이제곱분포 |
dchisq() |
pchisq() |
qchisq() |
rchisq() |
| 이항분포 |
dbinom() |
pbinorm() |
qbinorm() |
rbinorm() |
추정(신뢰구간)
개요
표본을 추출해서 전체 모집단의 성격을 추정하는 것이야 말로 통계의 전통적인 목적 가운데 하나라 하겠다. 이때 추정의 방법에는 다음 두 가지가 있다.
- 점 추정 : 단일 값으로 추정하는 것
- 구간 추정 : 일정한 구간을 두어 추정하는 것으로서 단측(one-sided) 구간추정과 양측(two-side) 구간추정으로 나뉜다.
단순하게 본다면 알고 있는 데이터의 평균을 통해 점 추정을 하는 것도 생각해 볼 수 있겠다.
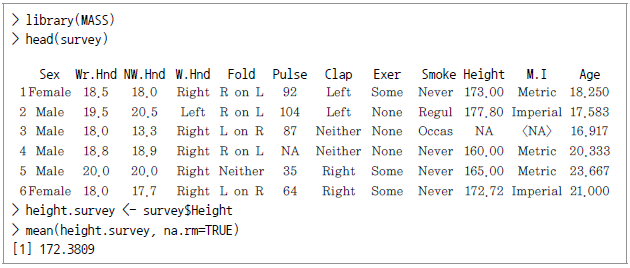
위는 MASS 패키지에 수록된 어느 대학의 학생에 관한 조사자료인데 키를 추정함에 있어 전체 학생의 평균으로 대체했다. 그러나 점추정은 너무 단순해 현실에서 추정치로 사용하는 데에는 한계가 있으므로 대신 각종 확률분포를 기반으로 한 구간추정을 중심으로 논의를 전개하려 한다.
우선 z-분포란 정규분포를 평균?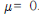 으로, 분산?
으로, 분산?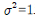 로 표준화시킨 것을 말하며 다음과 같이 정의된다.
로 표준화시킨 것을 말하며 다음과 같이 정의된다.
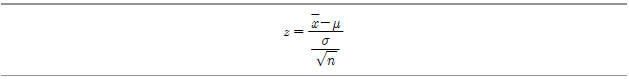
그리고 이 식을 변형하면 다음과 같이 신뢰구간을 표시할 수 있다.
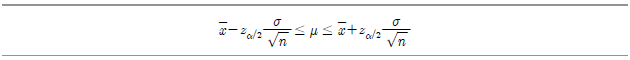
위 식은 모집단 평균
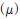
을 추정하기 위한?
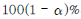
의 신뢰구간을 표현하고 있다. 여기서?
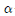
는 정규분포곡선에서 신뢰구간 밖의 영역을 뜻하고,?
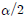
는 이러한 신뢰구간 밖의 영역 중 한쪽 끝(tail)을 나타낸다.
- 모집단 평균에 관한 신뢰구간 추정
- 모집단 데이터의 성격을 추정함에 있어서는 상황에 따라 다음과 같이 적용하는 통계량이 달라지게 된다.

우선 모집단의 표준편차를 알고 있으면서 모평균의 구간추정을 하는 경우를 살펴 본다.
예컨대 앞의 대학생 관련 자료와 관련해 학생의 키에 대한 모분산이 9.48인 상태에서 95%의 신뢰수준으로 구간 추정을 한다면 다음과 같다.
![> library(MASS) >height.response <-na.omit(survey$Height) > n<- length(height.response) >sigma <-9.48 >stderror <-sigma / sqrt(n) >stderror [1] 0.6557453](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_44.png)
한편 오차의 마진(margin of error)을 구하는 경우에는 주의가 필요하다. 즉 정규분포가 양측(2-tailed)이라는 점에서 95%의 신뢰수준이라 하면, 양쪽 꼬리부분이 각각 2.5%씩 차지할 것이다. 따라서?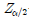 는 97.5%에 해당하고 여기에 stderror를 곱해서 구해야 한다.
는 97.5%에 해당하고 여기에 stderror를 곱해서 구해야 한다.
![> E <-qnorm(.975) * stderror >xbar <-mean(height.response) >xbar + c(-E, E) [1] 171.0956 173.6661](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_46.png)
또는 이러한 작업을 좀 더 간편하게 하기 위해서 다음과 같이 TeachingDemos 패키지를 이용할 수 있다.


다음으로 모분산을 모르는 가운데 모평균에 대한 구간추정을 하는 경우를 살펴본다. 이 경우에는 자유도 n-1인 student t-분포의?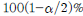 를 양단으로 하도록 구간추정을 실시한다. 앞의 대학생 통계자료를 이용해서 본다면 다음과 같다.
를 양단으로 하도록 구간추정을 실시한다. 앞의 대학생 통계자료를 이용해서 본다면 다음과 같다.
![> library(MASS) >height.response <-na.omit(survey$Height) > n <- length(height.response) > s <-sd(height.response) # sample standard deviation > SE <-s / sqrt(n); SE # Srandard error esimate [1] 0.6811677 > # > E <-qt(.975, df=n-1)*SE; E [1] 1.342878 > xbar + c(-E,E) [1] 171.0380 173.7237](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_49.png)
또는 일일이 계산해 구하는 대신 직접 t.test() 함수를 이용하면 편리하다.

- 모집단 비율에 관한 신뢰구간 추정
- 아래에는 앞의 예에서 여학생의 비율을 점추정하는 것과 구간추정하는 것을 차례로 보여주고 있다.

정규분포로부터 신뢰구간을 계산
정규분포는 자연현상에 가장 잘 부합하는 것으로서 통계분석의 기본을 이룬다. 여기서는 논의를 위해 표본의 평균이 5, 표준 편차가 2, 표본의 수가 20인 상태에서 유의도 수준은 95%를 가정하고 신뢰구간을 계산한다.
![> a <- 5 > s <-2 > n <-20 > error <-qnorm(0.975)*s/sqrt(n) > left <-a-error > right < -a+error > left [1] 4.123477 > right [1] 5.876523](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_53.png)
원래의 확률변수가 정규분포를 보이며 표본이 상호 독립적인 경우 진정한 평균값은 95% 확률로 4.12와 5.88 사이에 존재할 것으로 추정된다.
t-분포로부터 신뢰구간을 계산
t-검정을 통해 신뢰구간을 계산하는 것도 정규분포를 이용하는 것과 크게 다르지 않다. 차이가 있다면 정규분포 대신 t-분포를 적용할 뿐이다. 앞과 같이 논의를 위해 표본의 평균이 5, 표준 편차가 2, 표본의 수가 20인 상태에서 유의도 수준은 95%를 가정하고 신뢰구간을 계산한다.
![> a <- 5 > s <-2 > n <-20 > error <-qt(0.975, df=n-1)*s/sqrt(n) > left <-a-error > right <-a+error > left [1] 4.063971 > right [1] 5.936029](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_54.png)
원래의 확률변수가 정규분포를 보이며 표본이 상호 독립적인 경우 진정한 평균값은 95% 확률로 4.06에서 5.94 사이에 존재할 것으로 추정된다.
이제 단변량 데이터일 때 95% 유의수준으로 평균구간을 살펴보자(w1.dat라는 이름의 데이터셋을 이용한다)
![>w1 <- read.csv(file="w1.dat", sep=",", head=TRUE) > summary (w1) vals Min. : 0.130 1st Qu.:0.480 Median : 0.720 Mean : 0.765 3rd Qu.:1.008 Max. : 1.760 > length(w1$vals) [1] 54 > mean(w1$vals) [1] 0.765 > sd(w1$vals) [1] 0.3781222](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_55.png)
이제 우리는 평균에 대한 오차를 계산할 수 있다.
![> error <-qt(0.975, df=length(w1$vals)-1)*sd(w1$vals)/sqrt(length(w1$vals)) > error [1] 0.1032075](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_56.png)
평균에서 오차만큼 양쪽으로 벌리면 신뢰구간을 알아낼 수 있다.
![> left <- mean(w1$vals)-error > right <-mean (w1$vals)+error > left [1] 0.6617925 > right [1] 0.8682075](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_59.png)
원래의 확률변수가 정규분포를 하고 표본이 상호 독립적이라면 진정한 평균은 95% 확률로 0.66에서 0.87 사이에 존재한다고 하겠다.
t-분포로부터 여러 개의 신뢰구간을 계산하는 경우를 살펴 본다. 여러 번 검정을 하고 그 신뢰구간을 알고 싶은 경우로서 다음 3개의 서로 다른 결과치를 갖고 있다고 하자.
[표 Ⅳ-2-1] 검정 결과치
| Comparison 1 |
|
|
|
Mean |
Std. Dev. |
Number (pop.) |
| Group I |
10 |
3 |
300 |
| Group II |
10.5 |
2.5 |
230 |
| Comparison 2 |
|
|
|
Mean |
Std. Dev. |
Number (pop.) |
| Group I |
12 |
4 |
210 |
| Group II |
13 |
5.3 |
340 |
| Comparison 3 |
|
|
|
|
Mean |
Std. Dev. |
Number (pop.) |
| Group I |
30 |
4.5 |
420 |
| Group II |
28.5 |
3 |
400 |
이들 각각의 비교값과 관련하여 그 차이에 대한 상호 연관된 평균값의 신뢰구간을 알아 보고자 한다. 각 비교에는 2개의 그룹이 존재하는데 첫 번째 그룹으로부터의 결과를 위 비교표의 첫째 줄에, 그리고 두 번째 그룹의 결과는 둘째 줄에 기록한다. 우선 표준오차와 t-score를 계산한다.
첫째 그룹의 평균은 m1변수에 정의돼 있고 둘째 그룹의 평균은 m2에 정의돼 있다. 또한 첫째 그룹의 표준편차는 sd1에, 그리고 둘째 그룹의 표준편차는 sd2에 있다. 첫째 그룹의 표본의 크기는 num1, 둘째 그룹의 표본의 크기는 num2이다.
표준오차는 (sd1^2)/num1+(sd2^2)/num2의 제곱근이며, 다음과 같이 계산된다.

아래에서 이들 값을 확인하였다.
![> m1 [1] 10 12 30 > m2 [1] 10.5 13.0 28.5 > sd1 [1] 3.0 4.0 4.5 > sd2 [1] 2.5 53. 3.0 > num1 [1] 300 210 420 > num2 [1] 230 340 400 > se [1] 0.2391107 0.3985074 0.2659216 > error [1] 0.4711382 0.7856092 0.5227825](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_58.png)
이제 가정된 차이값에 관한 신뢰구간을 정의한다. 참고로 자유도를 계산하기 위해서 pmin 명령어를 사용하는데 이 경우 귀무가설은 차이가 없다는 것(즉, 0)으로서 유의도 수준은 95%를 이용한다.
![> left <- (m1-m2)-error > right <- (m1-m2)+error > left [1] -0.9711382 -1.7856092 0.9772175 > right [1] -0.02886177 -0.21439076 2.02278249](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_60.png)
위의 결과를 통해 확률변수가 정규분포를 갖고 표본이 상호독립적이라고 가정할 때 95% 유의도 수준에서 신뢰구간은 -0.97 와 -0.03 사이에 있음을 알 수 있다.
가설검정
개요
가설검정은 주장이나 가정을 명확히 설정하고 데이터를 통해 통계적으로 증명하는 것을 말하며, 통계분석의 중심 이론체계를 이루고 있다. 귀무가설과 대립가설로 나누어 진행을 하는데 진실과 이에 대한 의사결정의 관계는 다음의 표로 요약된다.
[표 Ⅳ-2-2] 제1종 오류와 제2종 오류 및 검정력
![[표 Ⅳ-2-2] 제1종 오류와 제2종 오류 및 검정력](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_61.png)
다음으로는 모집단의 통계량 조건을 일부 아는 경우와 그렇지 않은 경우로 나누어 살펴 본다.
모집단의 평균에 대한 가설검정
- 모집단의 분산을 알 때
- 우선 모집단 평균의 Lower Tail 검정의 귀무가설은 다음과 같다.

검정통계량?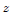 를 표본평균, 표본크기 및 모집단 표준편차를 이용해 정의한다면 다음과 같다.
를 표본평균, 표본크기 및 모집단 표준편차를 이용해 정의한다면 다음과 같다.
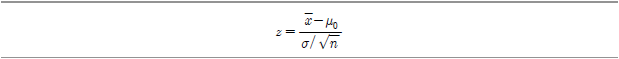
이 때?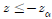 인 경우 lower tail 검정에 대한 귀무가설은 기각된다(단,
인 경우 lower tail 검정에 대한 귀무가설은 기각된다(단,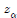 는 정규본포에서의 100(1
는 정규본포에서의 100(1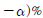 임), 전구 생산업체에서 전구의 수명이 1만 시간이라고 주장한다. 그런데 30개의 표본을 통해 살펴보니 평균 9,900시간 사용이 가능하다는 것을 발견했다. 모집단의 표준편차가 120시간이라고 가정한다면 유의도 수준 0.05를 기준으로 할 때 이 생산업자의 주장을 기각할 수 있을까?
임), 전구 생산업체에서 전구의 수명이 1만 시간이라고 주장한다. 그런데 30개의 표본을 통해 살펴보니 평균 9,900시간 사용이 가능하다는 것을 발견했다. 모집단의 표준편차가 120시간이라고 가정한다면 유의도 수준 0.05를 기준으로 할 때 이 생산업자의 주장을 기각할 수 있을까?
![> xbar = 9900 #(가설의) 표본평균 > sigma = 120 #(모집단의) 표준편차 > n = 30 #표본의 크기 > z=(xbar-mu0)/(sigma/sqrt(n)) # 검정통계량 > z [1] -41.5644 > We then compute the critical value at .05 significance level. > alpha = .05 > z.alpha = qnorm(1-alpha) > -z.alpha # critical value [1] -1.6449](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_68.png)
검정통계량 -4.5644는 임계치(critical value) -1.6449보다 작으므로 0.05의 유의도 수준에서 전구의 평균수명이 1만 시간이라는 귀무가설을 기각한다. 또 다른 계산방법으로는 임계치를 이용하는 대신 pnorm 함수를 이용해 검정통계의 lower-tail 을 계산할 수 있다. 다음은 0.05의 유의수준보다 작으므로 귀무가설을 기각함을 보여주고 있다.
![> pval = pnorm(z) > pval [1] 2.5052e-06 # 단측 p값](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_69.png)
반면 모집단 평균의 Upper Tail 검정은 앞의 좌측단측(lower tail) 검정과 반대의 평가 기준이 적용된다. 즉, 귀무가설은 다음과 같다.
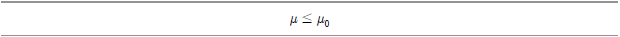
검정통계량?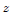 는 다음과 같다.
는 다음과 같다.

예를 들어 과자봉지에 붙어 있는 설명을 따르면, 쿠키과자 한 개에 최대 2그램의 포화지방이 들어 있다고 한다. 이때 35개의 과자를 표본으로 추출해 포화지방의 함유량을 살펴보니 평균 2.1 그램이 담겨 있었다. 모집단의 표준편차가 0.25그램이었다면 유의도 수준 0.05를 기준으로 할 때 이 생산업자의 주장을 기각해도 되는가를 살펴 보라.
![> xbar = 2.1 #표본평균 > mu0=2 #가설로 제시된 값 >sigma=0.25 #모집단의 표준편차 >n=35 #표본의 크기 >z=(xbar-mu0)/(sigma/sqrt(n)) #검정통계량 >z [1] 2.3664 > alpha = .05 > z.alpha = qnorm(1-alpha) > z.alpha [1] 1.6449 #임계치(critical value)](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_72.png)
검정통계량 2.3664가 임계치인 1.6449보다 크므로 0.05 유의도 수준에서 과자의 포화지방 함유량이 2그램이라는 귀무가설을 기각한다.
다른 방법
임계치를 이용하는 대신 pnorm 함수를 통해 검정통계의 우측단측 p-value를 계산할 수 있다.
아래에서 그 값이 0.05의 유의도 수준보다 작으므로 우리는?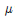 ?≤ 2라는 귀무가설을 기각한다
?≤ 2라는 귀무가설을 기각한다


남극의 킹 펭귄(황제 펭귄 다음으로 큰)의 평균몸무게는 15.4kg이었다. 같은 계절, 같은 지역에서 35마리를 표본으로 해 무게를 재 보니 14.6kg이었다. 모집단의 표준편차가 2.5kg이라고 가정하면 0.05의 유의도 수준에서 원래 펭귄의 평균무게와 작년의 평균무게가 다르지 않다는 귀무가설을 유지할 수 있는 것인지 또는 기각해야 하는 것인지 알아보라.
![>xbar = 14.6 #표본평균 >mu0 - 15.4 #가설수립에 적용된 값 >sigma = 2.5 #모집단의 표준편차 >n=35 #표본의 크기 >z=(xbar-mu0)/(sigma/sqrt(n)) #검정통계량 > z [1] -1.8931 > alpha = .05 > z.half.alpha = qnorm(1-alpha/2) > c(-z.half.alpha, z.half.alpha) [1] -1.9600 1.9600](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_77.png)
검정통계량 -1.8931이 임계치인 -1.9600과 1.9600 사이에 있으므로 0.05유의도 수준에서 펭귄의 무게가 작년과 달라졌다는 귀무가설을 기각하지 못한다. 임계치를 이용하는 대신 pnorm 함수를 통해 검정통계량의 양측 (two-tailed)의 p-value를 계산할 수 있다. 표본평균이 가설에서 제시된 값보다 작으므로 lower tail p-value는 두 배가 되었다. 결국 산출된 값이 0.05 유의수준보다 크므로?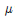 ?= 15.4라는 귀무가설을 기각하지 않는다.
?= 15.4라는 귀무가설을 기각하지 않는다.
![>pval = 2*pnorm(z) #lower tail > pval #two-taild p-value [1] 0.058339](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_78.png)
- 모집단의 분산을 모르는 경우
- 모집단 평균의 좌측단측 검정을 위한 귀무가설은 다음과 같다 (단,?
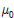 는 모평균?
는 모평균?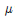 의 lower bound 추정치).
의 lower bound 추정치).
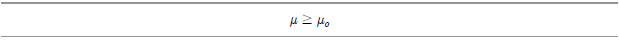

전구생산업체에서 전구의 수명이 1만 시간이라고 주장한다. 이때 30개의 표본을 통해 살펴보니 평균 9,900시간 동안 사용이 가능함을 발견했다. 모집단의 표준편차가 125시간이라고 가정한다면 유의도 수준 0.05를 기준으로 할 때, 이 생산업자의 주장을 기각할 수 있을까?
![> xbar = 9900 #표본평균 >mu0 = 10000 #가설수립에 적용된 값 > s = 125 #표본표준의 편차 >n = 30 #표본의 크기 > t = (x-bar-mu0)/(s/sqrt(n)) > t #표본통계량 [1] -4.3818 > alpha =.05 >t.alpha = qt(1-alpha, df=n-1) > -t.alpha = qt(1-alpha, df=n-1) > -t.alpha #critical value [1] -1.6991](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_81.png)
검정통계량 -4.3818이 임계치인 -1.6991보다 작으므로 0.05의 유의도 수준에서 전구수명이 1만시간이라는 귀무가설을 기각할 수 있다. 임계치를 이용하는 대신 pt함수를 통해 검정통계량의 좌측단측p-value를 계산할 수도 있다. 이 값이 0.05 유의수준보다 작으므로?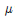 ?≥10000라는 귀무가설을 기각한다.
?≥10000라는 귀무가설을 기각한다.
![> pval = pt(t, df=n-1) > pval [1] 7.035e-05 #우측단측의 (lower tail)의 p-value](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_82.png)
한편 모집단 평균의 우측단측검정을 위한 귀무가설은 다음과 같다. (단,?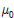 는 진정한 모집단 평균
는 진정한 모집단 평균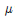 에 관한 가설에서 제시된 upper bound다).
에 관한 가설에서 제시된 upper bound다).
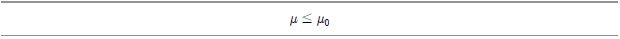
검정통계량 t를 표본평균, 표본의 크기 및 표본의 표준편차?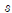 에 대해 정의하면 다음과 같다.
에 대해 정의하면 다음과 같다.

과자봉지에 붙어 있는 설명을 따르면, 쿠키과자 한 개에 최대 2그램의 포화지방이 들어 있다고 한다. 이때 35개의 과자를 표본으로 추출해 포화지방 함유량을 살펴보니 평균 2.1그램이 들어 있었다. 표본의 표준편차가 0.3그램이었다면 유의도 수준 0.05를 기준으로 할 때, 이 생산업자의 주장을 기각해도 되는가를 살펴보라.
![>xbar = 2.1 #표본평균 >mu0 = 2 #가설수립에 적용된 값 > s = 0.3 #표본표분편차 > n = 35 #표본의 크기 > t = (x-bar-mu0)/(s/sqrt(n)) #t 검정통계량 >t [1] 1.9720 > alpha = .05 >t.alpha=qt(1-alpha, df=n-1) >t.alpha [1] 1.69941 #critical value](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_85.png)
검정통계량 1.9720가 임계치 1.6991보다 크므로 0.05 유의도 수준에서 과자에 포함된 포화지방의 함유량이 2 그램이라는 귀무가설을 기각할 수 있다.
임계치를 계산하는 대신 pt함수를 통해 검정통계의 우측단측의 p-value를 계산할 수 있다. 아래에서 보듯 그 값이 0.05 의 유의도 수준보다 작으므로?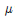 ?≤ 2라는 귀무가설을 기각한다.
?≤ 2라는 귀무가설을 기각한다.
![>pval = pt (t, df=n-1, lower.tail = FALSE) >pval [1] 0.028393 #우측단측의 p값](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_86.png)
모집단 평균의 양측검정 wo-tailed 검정을 위한 귀무가설은 다음과 같다(단,?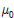 는 실제 모집단 평균?
는 실제 모집단 평균?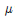 의 추정치).
의 추정치).
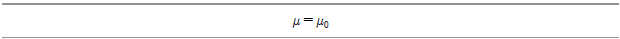
이러한 통계량 t를 표본평균, 표본크기 및 표본의 표준편차?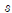 를 기준으로 정의하면 다음과 같다.
를 기준으로 정의하면 다음과 같다.

남극의 킹 펭귄(황제 펭귄 다음으로 큰)의 평균 몸무게는 15.4kg이었다. 같은 계절, 같은 지역에서 35마리를 표본으로 해 무게를 재 보니 14.6 kg이었다. ‘표본’의 표준편차가 2.5kg이라고 가정하면 0.05의 유의도 수준에서 다음의 귀무가설을 유지할 수 있을 것인지 또는 기각해야 하는 것인지 알아보라. 귀무가설: 원래의 펭귄의 평균무게와 작년의 평균무게가 다르지 않다(즉,?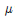 ?= 15.4).
?= 15.4).
![> xbar = 14.6 > mu0 = 15.4 > s = 2.5 > n = 35 > t = (xbar-mu0)/(s/sqrt(n)) > t [1] -1.8931 > alpha = .05 > t.half.alpha = qt(1-alpha/2, df=n-1) > c (-t.half.alpha, t.half.alpha) [1] -2.0322 2.0322](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_89.png)
통계량 -1.8931는 두 임계값 -2.0322와 2.0322 사이에 있다. 따라서 0.05의 유의도 수준에서 귀무가설을 기각하지 않는다.
다른 방식
임계치를 이용하는 대신 pt() 함수를 이용해 양측검정의 p-value를 계산할 수 있다.
다만 좌측 단측검정의 p-value를 2배로 조정해야 양측검정량이 된다는 점에 유의한다. 계산결과 유의도 수준인 0.05보다 크므로 귀무가설을 기각하지 않고 유지한다.
![> pval = 2 * pt(t, df=n-1) > pval [1] 0.066876 #양측검정의 p-value](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_90.png)
모집단 비율에 관한 가설검정
모집단 비율의 좌측단측 검정을 위한 귀무가설은 다음과 같다(단,?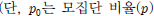 의 추정치 하한 (lower bound)이다.
의 추정치 하한 (lower bound)이다.
검정통계량으로서의?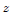 를 표본비율과 표본의 수로 정의하면 다음과 같다.
를 표본비율과 표본의 수로 정의하면 다음과 같다.
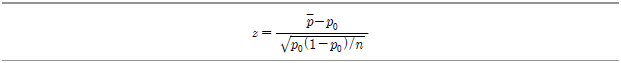
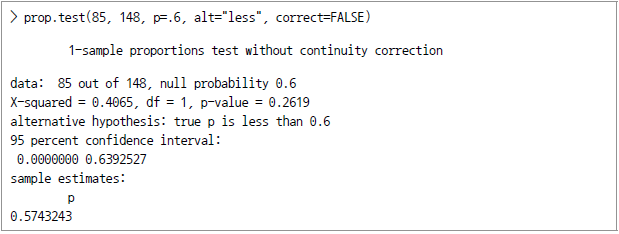
이제?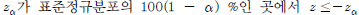 일 경우 좌측의 단측검정에 대한 귀무가설을 기각할 수 있게 된다. 예를 들어 살펴 보자. 지난 번 선거에서는 60%의 유권자가 투표에 참가하였다. 이번 선거의 경우 전화설문조사에서 148명 중 85명이 투표에 참여하였다고 응답하였다. 0.05의 유의도 수준에서 다음의 귀무가설을 기각할 수 있는지 검정하라.
일 경우 좌측의 단측검정에 대한 귀무가설을 기각할 수 있게 된다. 예를 들어 살펴 보자. 지난 번 선거에서는 60%의 유권자가 투표에 참가하였다. 이번 선거의 경우 전화설문조사에서 148명 중 85명이 투표에 참여하였다고 응답하였다. 0.05의 유의도 수준에서 다음의 귀무가설을 기각할 수 있는지 검정하라.
귀무가설: 올해도 최소한 60%의 유권자가 선거에 참여한다.
![> xbar = 14.6 > mu0 = 15.4 > s = 2.5 > n = 35 > t = (xbar-mu0)/(s/sqrt(n)) > t [1] -1.8931 > alpha = .05 > t.half.alpha = qt(1-alpha/2, df=n-1) > c(-t.halt.alpha, t.half.alpha) [1] -2.0322 2.0322](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_95.png)
다른 방식 1
임계치를 이용하는 대신 pnom() 함수를 이용해서 표본 변량의 좌측단측의 p-value를 계산할 수 있는데 계산결과 0.05의 신뢰도 수준보다 크므로 우리는 귀무가설을 기각하지 않고 유지한다.
![> pval = pnorm(z) > pval [1] 0.2618 #lower tail p-value](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_96.png)
다른 방식 2
prop.test() 함수를 이용해 직접 구할 수도 있다.
모집단 비율의 우측단측 검정을 위한 귀무가설은 다음과 같다.

이제 표본변량?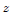 를 표본비율과 표본크기로 정의하면 다음과 같다.
를 표본비율과 표본크기로 정의하면 다음과 같다.
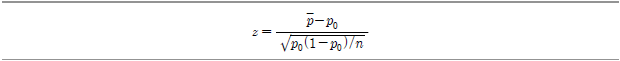
지난해에 과수원에서 수확한 사과 중 12%가 썩었다. 올해에 총 214개의 사과 중 30개가 썩은 것으로 판명되었다면 유의도수준 0.05를 기준으로 할 때 다음의 귀무가설을 기각할 수 있을까?
귀무가설: 올해는 썩은 사과의 비율이 12% 미만이다.
![> pbar = 30/214 > p0 = .12 > n = 214 > z = (pbar-p0)/sqrt(p0*(1-p0)/n) > z [1] 0.90875 > alpha = .05 > z.alpha = qnorm(1-alpha) > z.alpha [1] 1.6449](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_100.png)
위에서 표본통계량 0.90875가 임계치 1.6449보다 작으므로 0.05의 유의도 수준에서 썩은 사과의 비율이 올해는 12% 이하라는 귀무가설을 기각하지 않고 유지한다.
다른 방식 1
임계치를 이용하는 대신 pnorm() 함수를 이용해서 우측단측의 p-value를 구할 수 있다. 그 결과 0.05의 유의도 수준보다 크므로 귀무가설 ( p ≤ 0.12 )을 기각하지 않는다.
![> pval = pnorm(z, lower.tail = FALSE) > pval [1] 0.18174 #upper tail p-value](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_101.png)
다른 방식 2
prop.test () 함수를 이용해 p-value를 직접 구할 수 있다.

모집단 비율의 two-Tailed 검정을 위한 귀무가설은?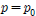 이며 표본통계량?
이며 표본통계량?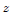 를 표본비율과 표본 크기를 기준으로 정의하면 다음과 같다.
를 표본비율과 표본 크기를 기준으로 정의하면 다음과 같다.

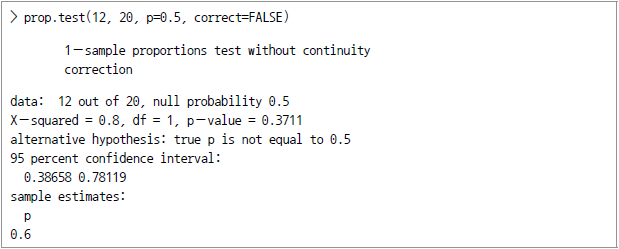
![> pbar = 12/20 > p0 = .5 > n = 20 > z = (pbar-p0)/sqrt(p0*(1-p0)/n) > z [1] 0.89443 > alpha = .05 > z.half.alpha.=qnorm(1-alpha/2) > c(-z.half.alpha, z.half,alpha) [1] -1.9600 1.9600](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_105.png)
표본통계량 0.89443가 임계치 -1.9600과 1.9600 사이에 있으므로 0.05의 신뢰수준에서 귀무가설을 기각하지 않는다.
다른 방식 1
임계치를 이용하는 대신 pnorm() 함수를 이용해서 양측검정의 pvalue를 구할 수 있다. 이때는 우측단측의 p-value가 두 배로 늘어난다. 계산 결과 0.05 유의도 수준보다 크므로 귀무가설을 기각하지 않는다.
![> pval = 2*pnorm(z, lower.tail = FALSE) #upper tail >pval [1] 0.37109 #양측검정의 p-value](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_106.png)
다른 방식 2
prop.test 함수를 이용할 수도 있다.
2개 대응표본 사이의 모집단 평균
대응표본(Matched Samples)이란 동일한 대상에 대해 반복적인 관측을 실시하는 경우를 말한다. 여기서 모집단은 정규분포를 한다고 가정한다. 대응 t-검정(paired t-test)을 통해 모집단 평균의 차이에 대해 추정할 수 있다.
여기서는 R에 내장된 immer 데이터 세트를 예로 이용한다. 이 데이터는 1931년부터 1932년 사이의 보리 수확량에 관한 데이터다.

immer의 데이터가 정규분포를 한다고 가정하고 95%의 유의도 수준에서 1931년과 1932년의 보리 수확량의 차이에 관한 신뢰구간을 추정하라.
우리는 다음과 같이 t.test 함수를 이용해 대응표본 평균값의 차이를 계산할 수 있다. 이 경우 비교검사(a paired test)이므로 "paired" argument를 TRUE로 지정했다.


위의 작업을 통해 immer 데이터 세트가 1931년에서 1932년 사이에 보리 수확량 차이의 95% 신뢰구간이 6.122와 25.705 사이임을 알 수 있다.
한편 여기서 가설검정에서 가장 많이 사용되는 t.test 함수에 대해 살펴보면 다음과 같다.
![[함수표준형] t.test(x, y = NULL, alternative = c("two.sided", "less", "greater"), mu = 0, paired = FALSE, var equal = FALSE, conf.level = 0.95, ...) [옵션 파라미터] x, y = 데이터 수치값 alternative = 대립가설에 대해 양측검정을 할 것인지 또는 단측검정을 할 것인지의 지정 mu = 표준값(또는 두 개의 표본이 있는 경우는 이들 각각 표준값의 차이) paired = 대응표본인지 여부 var.equal = 분산값을 같은 것으로 처리할지 여부 (TRUE인 경우에는 통합분산 (pooled variance)를 통해 분산을 추정한다. conf.level = 구간의 신뢰도](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_111.png)
2개 독립 표본(independent Samples) 사이의 모집단 평균
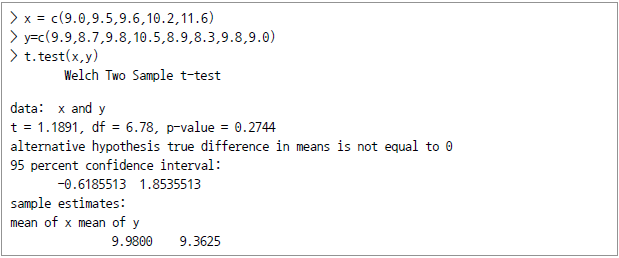
2개의 데이터 표본이 상호 독립적이라 함은 그 각각이 추출된 모집단이 서로 관련돼 있지 않으면서 표본들 간에도 서로 영향을 주지 않는 것을 말한다. 여기서 모집단은 정규분포를 한다고 가정한다. 비대응 t-검정(unpaired t-test)을 통해서 모집단 평균의 차이에 대해 추정할 수 있다.
내장 데이터 세트인 mtcars의 mpg 데이터프레임에는 1974년의 각종 자동차별 마일리지 데이터가 담겨 있다. 한편 am이라는 또 다른 column에는 변속장치의 종류(mission type)가 표기돼 있다(0 = automatic, 1 = manual).
특히 수동식과 자동 변속장치별 휘발유 마일리지는 상호 독립한 데이터다. 만약 mtcars 데이터가 정규분포를 한다고 가장할 때, 수동식과 자동식 변속장치 사이의 마일리지 차이에 대한 95%의 신뢰구간을 알아보자.
![> mtcars$am [1] 1 1 1 0 0 0 0 0 ... > L = mtcars$am = 0 > mpg.auto = mtcars[L,]$mpg > mpg.auto #자동변속장치의 마일리지 [1] 21.4 18.7 18.1 14.3 24.4 ... By applying the negation of L, we can find the gas mileage for manual transmission. > mpg.manual = mtcars[!L,]$mpg > mpg.manual #수동변속기의 마일리지 [1] 21.0 21.0 22.8 32.4 30.4 ... We can apply the t.test function to compute the difference in means of the two sample data. > t.test(mpg.auto, mpg.manual) Welch Two Sample t-test data: mpg.auto, mpg.manual t=-3.7671, df = 18.332, p-value = 0.001374 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -11.2802 -3.2097 sample estimates: mean of x mean of y 17.147 24.392](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_112.png)
mtcars에서 자동변속장치의 평균 마일리지는 17.147mpg이고 수동식의 경우에는 평균 마일리지가 24.392 mpg다. 이들의 수치 차이에 대한 95%의 신뢰구간은 3.2097부터 11.2802 mpg 사이임을 알 수 있다. 이와 달리 예측변수(predictor) mtcars$am에 의한 응답변수(mtcars$mpg)에 대한 모델을 설정한 후 t.test 함수를 적용함으로써 모평균의 차이에 대한 추정을 해 볼 수도 있다.

2개 모집단의 비율 비교에 관한 가설검정
서로 다른 2개 모집단에 대해 조사를 하고 이들 간의 응답비율을 비교하는 경우가 있다. 여기서 우리는 모집단이 정규분포를 하는 것으로 가정한다. 내장된 quine 데이터는 호주의 한 도시에 사는 어린이를 인종, 성별, 나이, 학습상태 및 학교 결시일수별로 분류한 데이터다.

여기서 Eth는 토착원주민 여부("A" or "N", 토착민을 aboriginal의 A로 표시)를 뜻하며 Sex는 성별("M" or "F")을 뜻한다. 이를 table() 함수를 이용해 인종배경과 성별에 따라 분류해 보니 그 결과는 다음과 같았다.

이제 quine 데이터가 정규분포를 가진다고 가정하고 토착민 여학생과 비토착민 여학생 간의 비율에 대한 95%의 신뢰구간을 추정하려면 다음과 같이 prop.test 함수를 이용하면 된다(단, 단순화를 위해 Yates의 연속성 보정(continuity correction)은 적용치 않음).
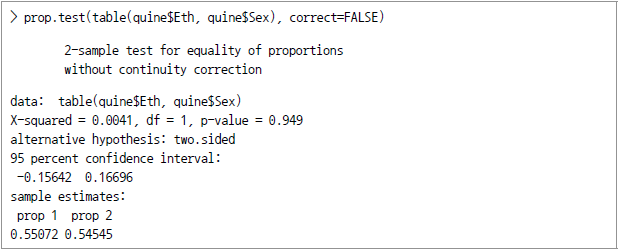
위 계산의 결과 토착민 여학생과 비토착민 여학생의 비율은 95% 유의수준을 갖는 신뢰구간이 -15.6%와 16.7%인 것으로 밝혀졌다.
p값의 계산
원래 p값이란 귀무가설이 맞다는 가정하에 검정통계량이 관측된 통계량 이상이 될 확률을 말하는 것으로서 관측된 유의수준 (observed significance level)이라고도 한다. 이하에서는 정규분포와 t- 분포를 가지는 예를 중심으로 p값의 계산방법을 살펴보고자 한다.
정규분포로부터 하나의 p값을 계산
논의를 위해 다음과 같은 가설에 대해 양측검정을 한다고 가정한다.
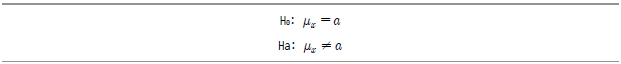
p값은 특정한 표본평균에 대하여 계산하는데 여기서는 계산된 표본평균이?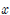 라고 가정한다. 즉, 이 경우의 p값이란 우리가 Z-score의 절대값보다 큰 (또는 Z-score의 음수값보다 작은) 표본평균을 얻을 확률을 뜻하게 된다.
라고 가정한다. 즉, 이 경우의 p값이란 우리가 Z-score의 절대값보다 큰 (또는 Z-score의 음수값보다 작은) 표본평균을 얻을 확률을 뜻하게 된다.
특히 정규분포의 경우에는 표준편차 값이 필요한데 우리는 표준편차가 s라고 주어졌을 때의 정규분포에서의 p값을 구하는 방법을 살펴보자. 이 경우 두 가지 방법이 가능한데 첫째 방법은 표본평균을 Z-score로 변환하여 이용하는 것이고, 둘째 방법은 단순히 표준편차를 지정한 후 컴퓨터가 계산하게 하는 것이다.
우선 Z-score를 이용해 p값을 계산하는 방법을 살펴본다. Z-score는 귀무가설이 맞다는 것을 전제로 하고 계산된다. 일단 Z-score를 알아내면, 그 값이 Z-score보다 작을 확률을 pnorm 명령어를 통해 계산할 수 있다.13) 그리고 나아가서 Z-score가 양수값으로 판명되면 1에서 해당 확률값을 빼야 한다. 또한 양측검정에서는 그 결과값에 2를 곱해야 한다.
아래의 예에서는 a=5, 표준편차 = 2, 표본의 크기는 20이라고 하고 표본평균=7에 대한 p값을 계산한다.
![> a <-5 > s <-2 #표준편차 > n <-20 #표본의 크기 > xbar <-7 #표본의 평균 > z <-(xbar-a)/(s/sqrt(n)) >z [1] 4.472136 > 2*pnorm(-abs(z)) [1] 7.744216e-06](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_118.png)
이제 같은 상황에서 두 번째 방법으로 소개했던 pnorm 명령어에 단지 평균과 표준편차를 지정하는 경우를 살펴본다. 다만, 이 경우에는 단순히 좌측단측 (left-tail)만 이용하는 것은 적절치 않다. 표본평균이 당초 가정했던 평균보다 큰 값을 가지기 때문에 2 x (1-해당확률)로 변환하는 것이 필요하다.
![> a <-5 > s < -2 > n <-20 > xbar <-7 > 2*(1-pnorm(xbar, mean=a, sd=s/sqrt(20))) [1] 7.744216e-06](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_119.png)
t-분포로부터 하나의 p값을 계산
t-분포를 이용해 p값을 찾아내는 것은 앞서 Z-score를 이용하는 것과 유사하다. 단지 자유도를 지정해야 한다는 차이가 있을 뿐이다.
![> a <-5 > s <-2 > n <-20 > xbar <-7 > t <-(xbar-a)/(s/sqrt(n)) > t [1] 4.472136 > 2*pt(-abs(t), df=n-1) [1] 0.0002611934](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_120.png)
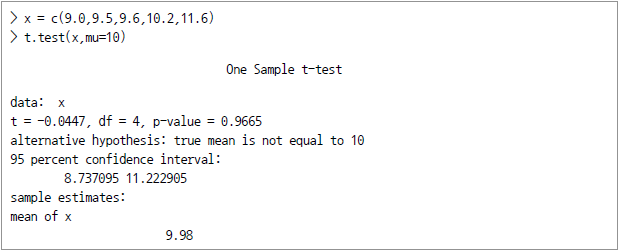
이제 단변량 데이터를 가지고 p값을 계산하는 예를 살펴본다. 여기서 우리는 w1.dat 데이터 세트를 이용한다.
![> w1 <-read.css(file="w1.dat", sep=",", head=TRUE) > summary(w1) Min. : 0.130 / 1st Qu. : 0.480 / Median : 0.720 / Mean : 0.765 / 3rd Qu. : 1.008 / Max. :1.760 > length(w1$vals) [1] 54](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_123.png)
이제 양측(two sided)의 가설검정을 해 본다.
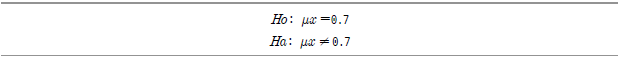
이제 p값의 계산을 위해 표본의 평균과 표준편차를 계산한다.
![> t <- (mean(w1$vals)-0.7)/(sd(w1$vals)/sprt(length(w1$vals))) > t [1] 1.263217 > 2*pt(-abs(t), df=length(w1$vals)-1) [1] 0.21204](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_122.png)
t-분포로부터 여러 개의 p값을 계산
여러 번의 검정에 대한 p값을 계산하는 경우에는 R과 같은 소프트웨어가 필수적이다. 여기서는 3회의 검정을 실시하고 이들간의 비교에 관한 단측의 가설검정(one-sided hypothesis test)을 해 보고자 한다. 이들 가설은 각각 다음의 형태를 띤다.
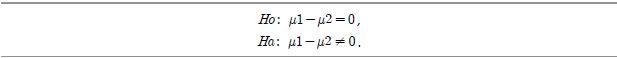
다음과 같이 3회의 비교실험을 했다고 가정한다.
[표 Ⅳ-2-3] 3회의 비교실험 결과
| Comparison |
Mean |
Std. Dev. |
Number (pop.) |
| Group I |
10 |
3 |
300 |
| Group II |
10.5 |
2.5 |
230 |
| Comparison |
Mean |
Std. Dev. |
Number (pop.) |
| Group I |
12 |
4 |
210 |
| Group II |
13 |
5.3 |
340 |
| Comparison |
Mean |
Std. Dev. |
Number (pop.) |
| Group I |
30 |
4.5 |
420 |
| Group II |
28.5 |
3 |
400 |
각각의 비교작업에 있어 2개의 그룹이 존재한다. 첫째 그룹의 결과는 각 실험 데이터의 첫째 줄에 기록돼 있고, 둘째 그룹의 결과는 둘째 줄에 기록돼 있다. 첫째 그룹의 평균은 m1에, 둘째 그룹의 평균은 m2에 저장한다. 첫째 그룹의 표준편차는 sd1에, 둘째 그룹의 표준편차는 sd2에 저장한다. 끝으로 표본의 개수는 각각 num1과 num2다.
먼저 표준편차와 t-score를 계산하는데 한꺼번에 이 작업을 수행하기 위해 일반 공식을 적용하기로 한다. 표준오차는 (sd1^2)/num1+(sd2^2)/num2의 제곱근이고 이에 관한 t-score는 (m1 - m2) /standard error다.
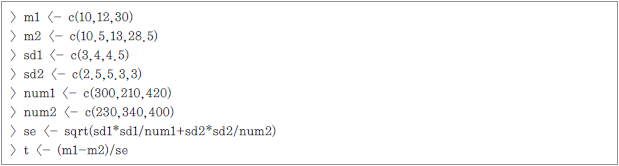
각 변수 값을 살펴 보았다.
![> m1 [1] 10 12 30 > m2 [1] 10.5 13.0 28.5 > sd1](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_126.png)
![[1] 3.0 4.0 4.5 > sd1 [1] 2.5 5.3 3.0 > num1 [1] 300 210 420 > num2 [1] 230 340 400 > se [1] 0.2391107 0.3985074 0.2659216 > t [1] -2.091082 -2.509364 5.640761](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_127.png)
pt 명령을 이용하기 위해서는 자유도를 지정해야 하는데, pmin 명령을 통해 다음과 같이 찾아낼 수 있다. 결국 우리가 찾는 p값은 다음의 명령을 통해 계산된다.
![>pt (t, df=pmin(num1, num2)-1) [1] 0.01881168 0.00642689 0.99999998](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_128.png)
이들 명령을 수행하면서 마지막에 있는 p값은 올바른 값이 아님을 알 수 있다. pt 명령어는 지정된 t보다 작은 값을 가질 확률을 계산한다. 여기서는 마지막 값이 양수로서 t-socre가 더 클 확률을 얻고자 하는 것이기 때문에 다음과 같이 변형해야 한다.
![> pt (-abs(t), df=pmin(num1, num2)-1) [1] 1.881168e-02 6.426890e-03 1.605968e-08](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_129.png)
간편 방법
t.test 명령을 통해 양측 가설검정을 간단히 수행할 수 있다.


이것은 지극히 당연한 결과라 하겠는데 만약 다른 평균값에 대해 계산한다면 mu 인자(argument)를 이용한다.
단측검정을 하는 경우에는 alternative 옵션을 지정하면 된다.

t.test() 명령에 데이터 세트를 추가하면 2개 데이터의 비교작업을 수행한다. 별다른 지정을 하지 않으면 상호 독립의 데이터로 계산되지만, 옵션 지정을 통해 의존성을 가진 데이터(dependent data sets)로 지정할 수도 있다.(help(t.test)를 통해 알아 본다)
적합도검정
적합도(Goodness-of-Fit)란 실험 또는 관찰로 얻은 결과가 이론과 일치하는 정도를 말한다.
카이제곱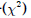 ?적합성 검정
?적합성 검정
데이터가 범주형(categorical)이고 서로 중복되지 않도록 나누어진 여러 개의 계급구간(class)에 속하는 경우 이를 다항(multinomial)형이라고 부른다. 다항분포에서의 적합성 검정을 위한 귀무가설은 관측된 빈도수?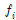 가 각각의 범주에 대한 기대값 e와 동일하다고 하는 것이다. 만약 다음의?
가 각각의 범주에 대한 기대값 e와 동일하다고 하는 것이다. 만약 다음의?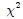 검정통계량의 p-value가 주어진 유의도 수준보다 작다면 이는 기각된다.
검정통계량의 p-value가 주어진 유의도 수준보다 작다면 이는 기각된다.
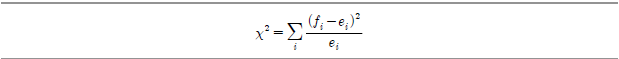
앞서 제시했던 survey 데이터를 다시 이용한다. 이 데이터는 원래 MASS 패키지에 포함된 것으로서 학생 흡연자들에 대한 것이다. 여기서 smoke 컬럼에는 학생들의 흡연 관련 데이터가 기록돼 있다. levels() 명령을 통해 볼 때 다음 "Heavy", "Regul" (regularly), "Occas" (occasionally) 및 "Never"의 4개 중 하나를 가짐을 알 수 있다.
![> library(MASS) > levels(survey$Smoke) [1] "Heavy" "Never" "Occas" "Regul"](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_136.png)
이제 우리는 table() 명령을 통해 빈도수를 요약해 보기로 한다.

이제 대학에서의 흡연에 관한 통계조사 결과가 다음과 같다면 0.05의 유의도 수준에서 실제로 표본이 이를 지지하는지 검정하라.

한편 여기서 카이제곱검정을 위한 chisq.test 함수를 잠시 살펴보면 다음과 같다.
![[함수 표준형] chisq.test(x, y = NULL, correct = TRUE, p=rep(1/length(x)), rescale.p=FALSE, simulate.p.value = FALSE, B=2000) [옵션 파라미터] x, y = 수치 벡터 또는 매트릭스(단, x, y는 동시에 factor 값도 가능) correct = 2x2 테이블에 대한 검정통계 계산 시 연속성수정(continuity correction)을 적용할지 여부 p=x에 대한 확률벡터 rescale.p = p값에 대해 rescale 작업을 할지 여부 simulate.p.value=p값을 계산함에 있어 Monte Carlo 시뮬레이션을 적용할지 여부 B=Monte Carlo 시뮬레이션을 적용할 때의 replicate의 개수 지정](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_139.png)
카이제곱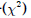 ?독립성 검정
?독립성 검정
2개의 확률변수?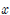 와?
와? 가 있을 때 한 변수의 확률분포가 다른 변수의 확률분포에 의해 영향 받지 않는다면 이들은 상호 독립적(independent )이라고 부른다.?
가 있을 때 한 변수의 확률분포가 다른 변수의 확률분포에 의해 영향 받지 않는다면 이들은 상호 독립적(independent )이라고 부른다.?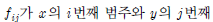 ?범주에 동시에 속하는 경우의 관측된 빈도수라고 가정한다. 또한?
?범주에 동시에 속하는 경우의 관측된 빈도수라고 가정한다. 또한?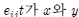 ?서로 독립적인 경우의 기대되는 count라고 가정한다. 이때 만약 다음의?
?서로 독립적인 경우의 기대되는 count라고 가정한다. 이때 만약 다음의?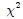 검정통계량의 p값이 주어진 유의도수준?
검정통계량의 p값이 주어진 유의도수준?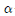 보다 작다면 독립성 가정에 대한 귀무가설은 기각된다.
보다 작다면 독립성 가정에 대한 귀무가설은 기각된다.

앞의 survey 데이터에서 흡연에 관한 Smoke 컬럼 이외에 Exer 컬럼에는 운동에 관한 데이터가 기록돼 있다. Smoke에서는 허용되는 값이 "Heavy", "Regul" (regularly), "Occas" (occasionally) 및 "Never"인 반면 Exer에서는 "Freq" (frequently), "Some", "None" 중 하나다. 이들을 표에 정리해 기록해 놓은 것을 분할표(contingency table)라고 부른다.

이제 학생의 흡연습관은 학생의 운동 정도와 독립적이라는 것을 0.05의 유의도 수준에서 검정하라.
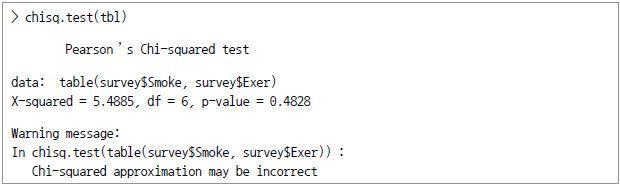
결국 p-value는 0.4828로서 0.05보다 크므로 귀무가설은 기각되지 않는다.
한편 앞에서 경고 메시지가 나온 이유는 cell 내의 값이 충분치 않기 때문이었다. 이를 피하려면 둘째와 셋째 컬럼을 합쳐서 새로운 테이블을 만들면 된다. 다음에 그러한 작업이 표시돼 있다.
![> ctbl = cbind(tbl[,"Freq"], tbl[,"None"] + tbl[,"Some"]) > ctbl > chisq.test(ctbl) Pearson's Chi-squared test data: ctbl X-squared = 3.2328, df = 3, p-value = 0.3571](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_145.png)
분산분석
분산분석은 2개 이상의 집단 간의 평균 차이를 검정할 때 사용한다. 집단 간의 평균 차이를 검정하기 위해 집단 간(between-group) 분산/ 집단 내(within-group) 분산의 비율을 사용하기 때문에 분산분석이라고 한다.
수집된 자료를 분석하는 것은 분산분석이지만 자료 자체를 어떻게 수집할 것인가가 선행되는데 이에 대한 것이 실험설계(experimental design)다. 실험설계란 가설검정을 할 수 있도록 계획하는 것으로서 그 과정에서 하나 또는 여러 개의 변수를 직접 제어할 수 있는 것을 말한다. 이때 독립변수는 처치변인(treatment variable)과 분류변인(classification variable으로서 기준변인이라고도 한다.)등으로 나눌 수 있다. 처치변인 실험자가 직접 통제하거나 변경시킬 수 있는 것을 말하는 반면, 분류변인은 실험 이전부터 존재하고 있기는 하지만 직접 통제할 수는 없는 것을 말한다.
완전임의배치법(일위 ANOVA , One-Way ANOVA)
처치변인을 실험단위에 배치하는 순서가 무작위(random)로 결정하는 것을 말한다. 수준 수가 k개이고 각 수준에 대해 r회의 반복을 시행한다면 전체실험은 k × r개로 분할하고 난수 등을 이용해서 확률적으로 배치하면 다음과 같이 귀무가설과 대립가설이 설정된다.

이러한 가설검정은 총분산을 다음의 항목으로 분할 (partition)하는 방식을 취한다.
- 처치변수 (treatment (columns))로 인한 분산
- 오차분산, 즉 처치변수로 설명되지 않는 분산
![[그림 Ⅳ-2-2] SST (총편차제곱합)의 구성](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_147.png)
[그림 Ⅳ-2-2] SST (총편차제곱합)의 구성

그리고 ANOVA에서는 처리변이와 오차변이를 비교해 F비율을 계산한다.

분산분석을 하려면 R에서는 aov() 또는 oneway.test() 함수를 사용한다. 우선 InsectSprays 데이터를 대상으로 aov() 함수를 이용한 분산분석의 예를 살펴 보자.
![[함수 표준형] aov(formula, data = NULL, projections = FALSE, qr = TRUE, contrasts = NULL, ...) [옵션파라미터] formula = 모델의 표현식 data = 적용 데이터 projections = projection을 반환할지 여부 qr = QR 분해를 반환할지 여부](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_150.png)
함수 적용식에 사용되는 부호는 다음과 같다.
[표 Ⅳ-2-4] 적용식에 사용되는 부호
| 부호 |
사용 |
| ~ |
모델에서의 설명변수와 응답변수를 구분 짓는다. 예컨대 Y ~ A + B + C 라면 Y라는 종속변수가 A, B, C에 의해 결정된다는 의미다. |
| + |
위에서 보았듯이 설명변수를 구분 지어 준다. |
| : |
설명변수들 사이에 상호작용(interaction)이 존재함을 의미한다. 예컨대 Y ~ A + B + A:B라면 Y가 A와 B에 의해 결정되는데, 이와 함께 A와 B 사이에는 상호작용이 존재함을 표시해 준다. |
| * |
변수 간에 완전 대응을 표시한다. 즉, Y ~ A*B*C라면 이는 Y ~ A + B + C + A:B + B:C + C:A + A:B:C를 의미한다. |
| ^ |
변수간의 차수를 지정한다. 일반식의 제곱에 대응하는 것으로 Y ~ (A+B+C)^2는 Y ~ A+B+C+A:B+A:C+B:C와 같은 의미가 된다. |
| . |
모든 변수가 다 동원된다는 뜻이다. 앞의 예를 기준으로 본다면 Y ~.는 Y ~ A+B+C를 의미한다. |
InsectSprays는 R에서 기본으로 제시되는 데이터로서 살충체의 종류(A~F)에 따라 해충의 수가 어떻게 바뀌는가를 보여주고 있다.
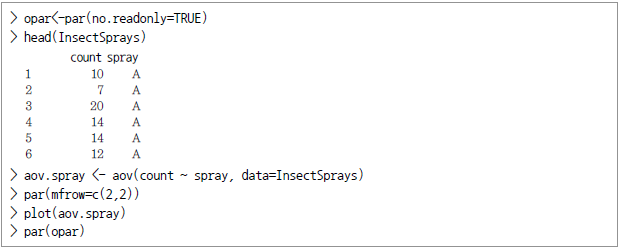
위 명령을 수행하면 분산모형이 수립(fit)되고 이와 관련한 4개의 그래프, 즉 잔차 vs. Fitted 값 도표, 정규성 검토 Q-Q plot, 표준 잔차의 제곱근과 적합값 도표 그리고 요인수준 대비 잔차 그래프등이 생성된다.
![[그림 Ⅳ-2-3] InsectSprays 데이터 세트에 대한 일위 ANOVA 분석결과](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_152.png)
[그림 Ⅳ-2-3] InsectSprays 데이터 세트에 대한 일위 ANOVA 분석결과
또 다른 예를 들어 본다. 어느 업체에서 3종의 신제품 출시를 앞두고 1개월 간 테스트 마케팅을 실시하였다. 그리고 이들 신제품에 따른 매출의 평균치가 동일한지를 0.05%의 유의수준 (significance level)으로 검증하고자 한다.
![> prod_A <-c(22, 42, 44, 52, 45, 37) > prod_B <-c(52, 33, 8, 47, 43, 32) >prod_c <-c(16, 24, 19, 18, 34, 39) > revenue <- cbind(prod_A, prod_B, prod_C) > r <-c(t(as.matrix(revenue))); r # r: response data [1] 22 52 16 42 33 24 44 8 19 52 47 18 45 43 34 37 32 39 >f <-c("Prodct A", "Prodct B", "Prodct C")](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_153.png)
![> k<-3 # number of treatment level > n <-6 # observations per treatment > tm <- gl(k, 1, n*km, factor(f)); tm [1] Prodct A Prodct B Prodct C Prodct A Prodct B Prodct C Prodct A Prodct B Prodct C Prodct A Prodct B [12] Prodct C Prodct A Prodct B Prodct C Prodck A Prodct B Prodct C Prodct A Prodct B Prodct C Prodct A Prodct B [12] Prodct C Prodct A Prodct B Prodct C Prodct A Prodct B Prodct C Levels: Prodct A Prodct B Prodct C > # apply aov() to a formula that describes r by treatment factor tm > av <- aov(r~tm) > # Print out the ANOVA table with the summary function. > summary (av) Df Sum Sq Mean Sq F value Pr(>F) tm 2 745.4 372.7 2.541 0.112 Residuals 15 2200.2 146.7](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_154.png)
위 예에서 우선 세 가지 제품별 판매액을 하나의 벡터로 만드는 작업이 진행됐다. 즉 as.matrix()를 통해 매트릭스 타입으로 변환한 후 t()를 적용해 열과 행을 바꾸는 전치행렬을 만들고 c()를 통해 하나의 벡터가 됐는데 이는 이 벡터를 모델에서의 응답 데이터로 이용하고자 함이다. 또한 처치수준을 f라는 이름의 factor 형으로 지정하고, 처리수준(treatment level)과 처치 별 관측 수를 지정한 후 gl()를 통해 factor의 수준을 지정했다. 그런 후 aov() 함수에 r ~ tm이라는 적용식(formula)으로 treatment factor를 통해 응답변수(r)가 얼마나 설명됐는지를 분석했다. 그 결과 p-value가 0.11이어서 앞서 지정한 유의수준 0.05보다 크므로 세 가지 신상품의 매출이 모두 같다는 귀무가설을 기각하지 않는다. 즉 검정결과 이들 사이에 사실상 별 차이가 없다는 결론을 내린다.
쌍별비교검정 또는 짝비교검정(Multiple Comparison Tests)
ANOVA는 그룹에서의 차이를 전반적으로 검정하는 것이다. 그런데 거기에 추가해 짝을 맞추어 시행하는 분석(pairwise analyses)을 통해 평균값의 어떤 부분이 특히(significantly) 다른지를 분석하는 기법이 있다. 대표적인 것이 Tukey의 HSD(Honestly Significant Difference) 검정과 Dunnett의 수정 Tukey-Kramer 다중검정(Pairwise Multiple Comparison Test)이다. 여기서는 Tukey의 HSD(Honestly Significant) 검정만을 살펴 본다. 먼저 aov()로 완전임의배치 단순분석을 하고, 같은 데이터에 대해 TukeyHSD() 함수를 통해 HSD 분석해 그 결과를 비교해 본다.

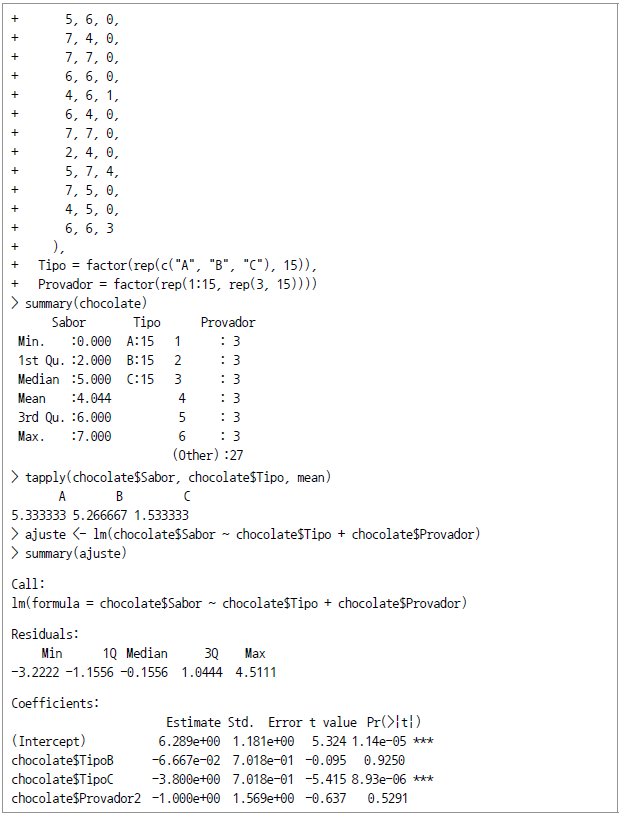
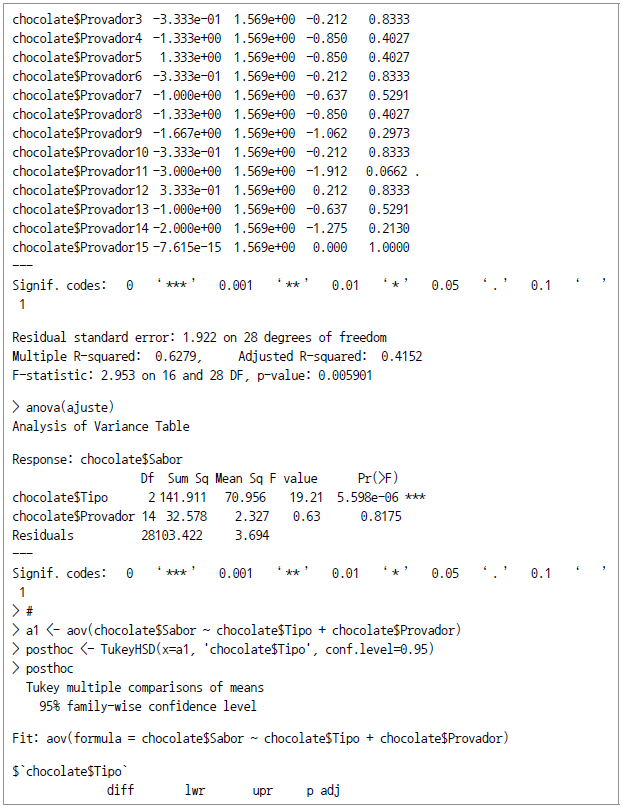
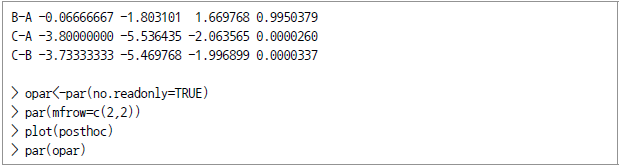
위 예에서는 tapply()를 통해 제품별 평점평균을 구하고 (A=5.33, B=5.27, C=1.53) aov() 명령을 적용해 보았다. 그 결과 평가자별(Provador) p-value는 0.8175가 나와서 평가자에 따른 점수 차이는 거의 없는 것으로 조사됐다. 다만 제품 타입(Tipo)별 분석 결과로는 p값이 매우 높은 것으로 나왔다. 그런데 Tukey의 HSD 분석 TukeyHSD() 명령을 적용하니 C와 A, C와 B 사이의 차이가 큰 것으로 (유의미한 것으로) 파악됐고 A와 B는 큰 차이가 없는 것으로 파악됐다.
![[그림 Ⅳ-2-4] chocolate$Tipo의 신뢰수준 차](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_159.png)
[그림 Ⅳ-2-4] chocolate$Tipo의 신뢰수준 차
무선화 구획설계
무선화 구획설계(無選化 區劃設計, Randomized Block Design)란 실험 설계방법의 하나로 피험자를 각 집단에 무선배치(random assignment)하여 비교집단 간의 동등성을 확보하고 이 과정에서 추가적으로 구획을 설정하는 방법이다. 이로써 동일구획 내에서는 각 집단에 동질적인 피험자들이 배치되는데, 구획은 종속변수와 상관이 높은 변수를 기준으로 설정되므로 구획 내의 피험자들은 반응(종속변수의 값)이 동질적이고 집단 내 분산을 구획에 의한 분산과 오차분산으로 분리하는 효과가 있다. 따라서 가설검정을 위한 오차분산(집단 내 평균자승합)이 축소돼 가설 검정력이 올라간다. 눈여겨 볼 것은 독립변수로서의 처치변수(treatment variable)에 구획변인(blocking variable)이 추가되는 것이다. 구획변인은 실험자가 통제할 수 없음에도 처치변수에 영향을 주는 변수를 말한다. 주된 관심은 아니지만 주된 분석을 보강하기 위해 지정되는 것이다.
![[그림 Ⅳ-2-5] 무선화 구획설계](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_160.png)
[그림 Ⅳ-2-5] 무선화 구획설계
참고로 무선화구획설계의 특수한 형태로 반복측정설계(反復測定設計, repeated measures design)가 있다. 동일한 피험자를 여러 가지 상이한 조건하에서 반복해 측정하는 실험설계법을 말하는데 실험분류법 중에서 가장 중요한 구분이 ‘피험자내 설계’(within-subject design)와 ‘피험자간 설계’ (between-subject design)다. 같은 피험자가 2회 이상의 처치를 받아 측정된다는 의미에서 전자인 ‘피험자내 설계’를 반복측정설계라고 부르기도 한다. 반복측정설계의 장점으로는 오차분산의 감소에 의한 F검정력 향상과, 필요로 하는 피험자의 수가 줄어든다는 점을 들 수 있다. 이 설계는 시간 경과에 따라 수행경향이 어떻게 변하는지를 알아보고자 할 때도 유용하다. 그러나 동일한 종속측정치의 반복된 사용은 연습효과에 따른 문제를 야기시킬 수 있다.
아래의 예에서는 어느 식품업체가 3개 신상품을 출시한 후 이들 각각의 평균매출이 사실상 동일하다고 할 수 있는지를 검정하고자 한다.

위에서는 3가지 상품의 처리수준(f=3종), 수준의 개수(k=3), 통제구획(n=6) 수를 할당한 후 처리 factor에 대한 벡터 데이터를 생성했다. 이어서 aov() 명령으로 처리 요인과 블록구획화변인에 따른 응답변수의 모델을 생성하고 그 결과를 summary() 함수로 조사했다.
그 결과 -value는 0.032로서 기준점으로 설정한 유의수준 0.05보다 작으므로 원래의 귀무가설은 기각되었다. 즉, 이 정도의 매출액이라면 3가지 신제품의 매출실적은 서로 상이한 것으로 판단된다.
![[그림 Ⅳ-2-6] 무선화구획설계에서의 총제곱합의 구성요소(SST = SSC + SSR + SSE)](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_162.png)
[그림 Ⅳ-2-6] 무선화구획설계에서의 총제곱합의 구성요소(SST = SSC + SSR + SSE)
요인분석적 설계
요인분석적 설계(要因分析的設計, factorial design)는 두 개 이상의 독립변인을 조작ㆍ통제해 이것이 종속변인에 주는 영향을 분석하기 위한 실험설계를 말한다. 예컨대 2×2 요인 설계는 두 독립변인이 각각 두 수준을 갖게 되고 결론적으로 네 개의 조건을 낳는 설계를 의미한다. 요인이란 각 독립변인의 모든 수준의 가능한 모든 조합이 검사된다는 것이다. 아래는 2-way 요인분석의 모습으로서 행과 열에 모두 처리변인이 적용되는 모습을 보여주고 있다.
![[그림 Ⅳ-2-7] 이위 (2-way) 요인분석](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_163.png)
[그림 Ⅳ-2-7] 이위 (2-way) 요인분석
일반적으로 요인설계는 단순 실험설계보다 많은 가설을 하나의 실험에서 적용하고 그 상호작용의 효과를 알 수 있다는 장점이 있다. 다음의 예는 R의 기본 데이터인 ToothGrowth를 대상으로 하고 있다. 이 데이터는 10명의 피실험자를 통해 3개 수준의 비타민C와 오렌지/아스코르브산(ascorbic acid)의 2가지 복용에 따른 치아모세포의 길이를 분석한 자료다.
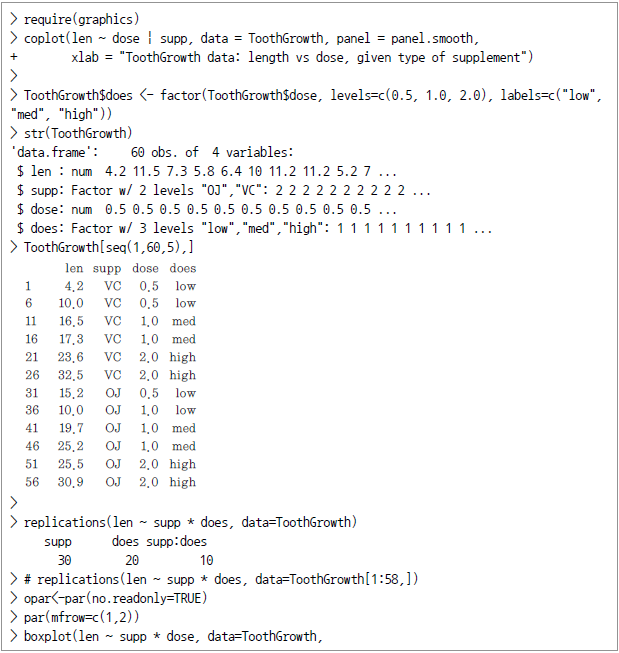

len 변수는 응답변수로서 이빨 (치아모세포)의 길이이며 supp는 보형물 관리를 어떤 성분으로 하였는지 (OC와 VC)를 뜻하고 dose는 몇 밀리그램을 적용했는지를 나타낸다. replications()는 적용식의 각 항(term)에 대해 replicate 벡터를 생성반환하는 함수인데, 이를 통해 균형설계 여부를 판단한다. 그리고 데이터를 시각적으로 표현하기 위해 boxplot() 명령과 interaction.plot() 명령을 적용했다.
![[그림 Ⅳ-2-8] 치아성장데이터의 상자도표(오른쪽 그림: 상호작용 도표)](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_166.png)
[그림 Ⅳ-2-8] 치아성장데이터의 상자도표(오른쪽 그림: 상호작용 도표)





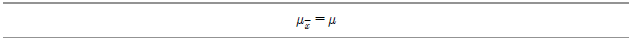
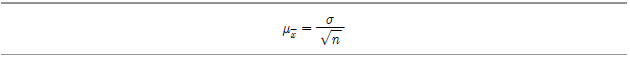
![[그림 Ⅳ-2-1] 표본 크기의 증가에 따른 표본평균분포곡선의 변화 모습](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_08.png)


![[함수 표준형] dnorm(x, mean = 0, sd = 1. log = FALSE) / pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE) / qnorm(p, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE) / rnorm(n, mean = 0, sd = 1), [옵션 파라미터] mean = 평균, sd = 표준편차, lower.tail = 좌측단측 여부, log = 확률이 log값으로 제시되는지 여부](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_11.png)
![]()
![> dnorm(0) [1] 0.3989423 > dnorm(0)*sqrt(2*pi) [1] 1 >dnorm(0, mean=4) [1] 0.0001338302 > dnorm(0, mean=4, sd=10) [1] 0.03682701 >v <- c(0,1,2) > dnorm(v) [1] 0.39894228 0.24197072 0.05399097 > x < - seq(-20,20,by=.1) > y <-dnorm(x) > plot(x,y) > y < - dnorm(x, mean=2.5, sd = 0.1) >plot(x,y)](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_13.png)
![> pnorm(0) [1] 0.5 > pnorm(1) [1] 0.8413447 > pnorm(0, mean=2) [1] 0.02275013 > pnorm(0, mean=2, sd=3) [1] 0.2524925 > v <- c(0,1,2) > pnorm(v) [1] 0.5000000 0.8413447 0.9772499 > x <- seq(-20, 20, by=.1) > y <-pnorm(x) >plot(x,y) > y <- pnorm(x, mean=3, sd=4) >plot(x,y)](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_14.png)
![> pnorm(0,lower.tail=FALSE) [1] 0.5 > pnorm(1, lower.tail=FALSE) [1] 0.1586553 > pnorm(0, mean=2, lower.tail=FALSE) [1] 0.9772499](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_15.png)
![>qnorm(0.5) [1] 0 > qnorm(0.5, mean=1) [1] 1 >qnorm(0.5, mean=1, sd=2) [1] 1 >qnorm(0.5, mean=2, sd=2) [1] 2 >qnorm(0.25, mean=2, sd=2) [1] 0.65101205 >qnorm(0.333) [1] -0.4316442 > qnorm(0.333, sd=3) [1] -1.294933 > qnorm(0.75, mean=5, sd=2) [1] 6.34898 > v = c(0.1, 0.3, 0.75) >qnorm(v) [1] -1.2815516 -0.5244005 0.6744898 > x <-seq(0,1,by=.05) > y <-qnorm(x) >plot(x,y) > y <-qnorm(x, mean=3, sd=2) >plot(x,y) > y <-qnorm(x, mean=3, sd=0.1) >plot(x,y)](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_16.png)
![> rnorm(4) [1] 1.2387271 -0.2323259 -1.2003081 -1.6718483 > rnorm(4, mean=3) [1] 2.633080 3.617486 2.038861 2.601933 > rnorm(4, mean=3, sd=3) [1] 4.580556 2.974903 4.756097 6.395894 > rnorm(4, mean=3, sd=3) [1] 3.000852 3.714180 10.032021 3.295667 > y <-rnorm(200) >hist(y) > y <-rnorm(200, mean=-2) >hist(y) >y <-rnorm(200, mean=-2, sd=4) >hist(y) >qqnorm(y) >qqline(y)](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_17.png)
![[함수표준형] dt(x, df=a) / pt(q, df=a) / qt(p, df=a) / rt(n, df=a), [옵션 파라미터] df = 자유도](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_18.png)

![> pt(-3,df=10) [1] 0.006671828 > pt(3, df=10) [1] 0.9933282 > 1-pt(3, df=10) [1] 0.006671828 >pt(3, df=30) [1] 0.996462 > x = c(-3, -4, -2, -1) >pt((mean(x)-2)/sd(x), df=40) [1] 0.000603064](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_20.png)
![> qt(0.05,df=10) [1] -1.812461 > qt(0.95, df=10) [1] 1.812461 > qt(0.05, df=20) [1] -1.724718 >qt(0.95, df=20) [1] 1.724718 > v <- c(0.005, .025, .05) >qt(v,df=253) [1] -2.595401 -1.969385 -1.650899 >qt(v,df=25) [1] -2.787436 -2.059539 -1.708141](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_21.png)
![> rt(3, df=10) [1] 0.9440930 2.1734365 0.6785262 > rt(3, df=20) [1] 0.1043300 -1.4682198 0.0715013 > rt(3, df=20) [1] 0.8023832 -0.4759780 -1.05461255](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_22.png)
![[함수표준형] dbinom(x, size, prob, log = FALSE) / pbinom(q, size, prob, lower.tail = TRUE, log.p = FALSE) / qbinom(p, size, prob, lower.tail = TRUE, log.p = FALSE) / rbinom(n, size, prob) [옵션파라미터] 앞서의 정규분포 관련 함수에서와 동일하다.](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_23.png)

![> pbinom(24,50,0.5) [1] 0.4438624 > pbinom(25, 50m 0.5) [1] 0.5561376 > pbinom(25, 51, 0.5) [1] 0.5 > pbinom(26, 51, 0.5) [1] 0.610116 > pbinom(25, 50, 0.5) [1] 0.5561376 > pbinom(25, 50, 0.25) [1] 0.999962 > pbinom(25, 500, 0.25) [1] 4.955658e-33](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_25.png)
![> qbinom(0.5, 51, 1/2) [1] 25 > qbinom(0.25, 51, 1/2) [1] 23 > pbinom(23, 51, 1/2) [1] 0.2879247 > pbinom(22. 51, 1/2) [1] 0.200531](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_26.png)
![> rbinom(5,100,.2) [1] 30 23 21 19 18 > rbinom(5, 100, .7) [1] 66 66 58 68 63](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_27.png)
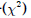 ?분포
?분포![[함수표준형] dchisq(x, df, ncp=0, log = FALSE) / pchisq(q, df, ncp = 0, lower.tail = TRUE, log.p = FALSE) / qchisq(p, df, ncp = 0, lower.tail = TRUE, log.p = FALSE) / rchisq(n, df, ncp = 0)](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_29.png)

![> pchisq(2,df=10) [1] 0.003659847 > pchisq(3, df=10) [1] 0.01857594 > 1-pchisq(3, df=10) [1] 0.981424 > pchisq(3, df=20) [1] 4.097501e-06 > x = c (2, 4, 5, 6) > pchisq(x, df=20) [1] 1.114255e-07 4.649808e-05 2.773521e-04 1.102488e-03](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_31.png)
![>qchisq(0.05, df=10) [1] 3.940299 > qchisq(0.95, df=10) [1] 18.30704 >qchisq(0.05, df=20) [1] 10.85081 > qchisq(0.95, df=20) [1] 31.41043 > v <-c(0.005, .025, .05) > qchisq(v, df=253) [1] 198.8161 210.8355 217.1713 > qchisq(v, df=25) [1] 10.51965 13.11972 14.61141](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_32.png)
![> rchisq(3,df=10) [1] 16.80075 20.28412 12.39099 > rchisq(3, df=20) [1] 17.838878 8.591936 17.486372 > rchisq(3, df=20) [1] 11.19279 23.86907 24.81251](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_33.png)

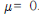 으로, 분산?
으로, 분산?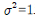 로 표준화시킨 것을 말하며 다음과 같이 정의된다.
로 표준화시킨 것을 말하며 다음과 같이 정의된다.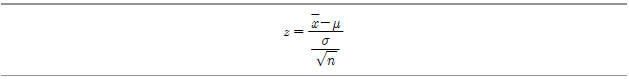
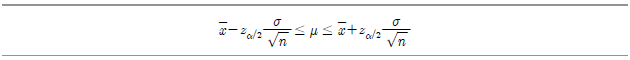
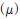 을 추정하기 위한?
을 추정하기 위한?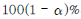 의 신뢰구간을 표현하고 있다. 여기서?
의 신뢰구간을 표현하고 있다. 여기서?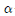 는 정규분포곡선에서 신뢰구간 밖의 영역을 뜻하고,?
는 정규분포곡선에서 신뢰구간 밖의 영역을 뜻하고,?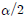 는 이러한 신뢰구간 밖의 영역 중 한쪽 끝(tail)을 나타낸다.
는 이러한 신뢰구간 밖의 영역 중 한쪽 끝(tail)을 나타낸다.![]()
![> library(MASS) >height.response <-na.omit(survey$Height) > n<- length(height.response) >sigma <-9.48 >stderror <-sigma / sqrt(n) >stderror [1] 0.6557453](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_44.png)
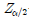 는 97.5%에 해당하고 여기에 stderror를 곱해서 구해야 한다.
는 97.5%에 해당하고 여기에 stderror를 곱해서 구해야 한다.![> E <-qnorm(.975) * stderror >xbar <-mean(height.response) >xbar + c(-E, E) [1] 171.0956 173.6661](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_46.png)


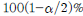 를 양단으로 하도록 구간추정을 실시한다. 앞의 대학생 통계자료를 이용해서 본다면 다음과 같다.
를 양단으로 하도록 구간추정을 실시한다. 앞의 대학생 통계자료를 이용해서 본다면 다음과 같다.![> library(MASS) >height.response <-na.omit(survey$Height) > n <- length(height.response) > s <-sd(height.response) # sample standard deviation > SE <-s / sqrt(n); SE # Srandard error esimate [1] 0.6811677 > # > E <-qt(.975, df=n-1)*SE; E [1] 1.342878 > xbar + c(-E,E) [1] 171.0380 173.7237](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_49.png)


![> a <- 5 > s <-2 > n <-20 > error <-qnorm(0.975)*s/sqrt(n) > left <-a-error > right < -a+error > left [1] 4.123477 > right [1] 5.876523](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_53.png)
![> a <- 5 > s <-2 > n <-20 > error <-qt(0.975, df=n-1)*s/sqrt(n) > left <-a-error > right <-a+error > left [1] 4.063971 > right [1] 5.936029](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_54.png)
![>w1 <- read.csv(file="w1.dat", sep=",", head=TRUE) > summary (w1) vals Min. : 0.130 1st Qu.:0.480 Median : 0.720 Mean : 0.765 3rd Qu.:1.008 Max. : 1.760 > length(w1$vals) [1] 54 > mean(w1$vals) [1] 0.765 > sd(w1$vals) [1] 0.3781222](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_55.png)
![> error <-qt(0.975, df=length(w1$vals)-1)*sd(w1$vals)/sqrt(length(w1$vals)) > error [1] 0.1032075](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_56.png)
![> left <- mean(w1$vals)-error > right <-mean (w1$vals)+error > left [1] 0.6617925 > right [1] 0.8682075](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_59.png)

![> m1 [1] 10 12 30 > m2 [1] 10.5 13.0 28.5 > sd1 [1] 3.0 4.0 4.5 > sd2 [1] 2.5 53. 3.0 > num1 [1] 300 210 420 > num2 [1] 230 340 400 > se [1] 0.2391107 0.3985074 0.2659216 > error [1] 0.4711382 0.7856092 0.5227825](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_58.png)
![> left <- (m1-m2)-error > right <- (m1-m2)+error > left [1] -0.9711382 -1.7856092 0.9772175 > right [1] -0.02886177 -0.21439076 2.02278249](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_60.png)
![[표 Ⅳ-2-2] 제1종 오류와 제2종 오류 및 검정력](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_61.png)

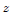 를 표본평균, 표본크기 및 모집단 표준편차를 이용해 정의한다면 다음과 같다.
를 표본평균, 표본크기 및 모집단 표준편차를 이용해 정의한다면 다음과 같다.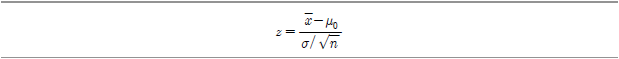
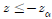 인 경우 lower tail 검정에 대한 귀무가설은 기각된다(단,
인 경우 lower tail 검정에 대한 귀무가설은 기각된다(단,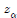 는 정규본포에서의 100(1
는 정규본포에서의 100(1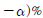 임), 전구 생산업체에서 전구의 수명이 1만 시간이라고 주장한다. 그런데 30개의 표본을 통해 살펴보니 평균 9,900시간 사용이 가능하다는 것을 발견했다. 모집단의 표준편차가 120시간이라고 가정한다면 유의도 수준 0.05를 기준으로 할 때 이 생산업자의 주장을 기각할 수 있을까?
임), 전구 생산업체에서 전구의 수명이 1만 시간이라고 주장한다. 그런데 30개의 표본을 통해 살펴보니 평균 9,900시간 사용이 가능하다는 것을 발견했다. 모집단의 표준편차가 120시간이라고 가정한다면 유의도 수준 0.05를 기준으로 할 때 이 생산업자의 주장을 기각할 수 있을까?![> xbar = 9900 #(가설의) 표본평균 > sigma = 120 #(모집단의) 표준편차 > n = 30 #표본의 크기 > z=(xbar-mu0)/(sigma/sqrt(n)) # 검정통계량 > z [1] -41.5644 > We then compute the critical value at .05 significance level. > alpha = .05 > z.alpha = qnorm(1-alpha) > -z.alpha # critical value [1] -1.6449](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_68.png)
![> pval = pnorm(z) > pval [1] 2.5052e-06 # 단측 p값](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_69.png)
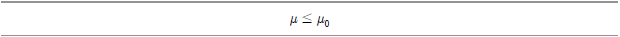
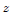 는 다음과 같다.
는 다음과 같다.
![> xbar = 2.1 #표본평균 > mu0=2 #가설로 제시된 값 >sigma=0.25 #모집단의 표준편차 >n=35 #표본의 크기 >z=(xbar-mu0)/(sigma/sqrt(n)) #검정통계량 >z [1] 2.3664 > alpha = .05 > z.alpha = qnorm(1-alpha) > z.alpha [1] 1.6449 #임계치(critical value)](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_72.png)
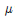 ?≤ 2라는 귀무가설을 기각한다
?≤ 2라는 귀무가설을 기각한다

![>xbar = 14.6 #표본평균 >mu0 - 15.4 #가설수립에 적용된 값 >sigma = 2.5 #모집단의 표준편차 >n=35 #표본의 크기 >z=(xbar-mu0)/(sigma/sqrt(n)) #검정통계량 > z [1] -1.8931 > alpha = .05 > z.half.alpha = qnorm(1-alpha/2) > c(-z.half.alpha, z.half.alpha) [1] -1.9600 1.9600](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_77.png)
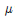 ?= 15.4라는 귀무가설을 기각하지 않는다.
?= 15.4라는 귀무가설을 기각하지 않는다.![>pval = 2*pnorm(z) #lower tail > pval #two-taild p-value [1] 0.058339](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_78.png)
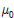 는 모평균?
는 모평균?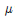 의 lower bound 추정치).
의 lower bound 추정치).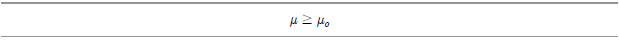

![> xbar = 9900 #표본평균 >mu0 = 10000 #가설수립에 적용된 값 > s = 125 #표본표준의 편차 >n = 30 #표본의 크기 > t = (x-bar-mu0)/(s/sqrt(n)) > t #표본통계량 [1] -4.3818 > alpha =.05 >t.alpha = qt(1-alpha, df=n-1) > -t.alpha = qt(1-alpha, df=n-1) > -t.alpha #critical value [1] -1.6991](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_81.png)
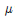 ?≥10000라는 귀무가설을 기각한다.
?≥10000라는 귀무가설을 기각한다.![> pval = pt(t, df=n-1) > pval [1] 7.035e-05 #우측단측의 (lower tail)의 p-value](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_82.png)
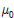 는 진정한 모집단 평균
는 진정한 모집단 평균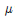 에 관한 가설에서 제시된 upper bound다).
에 관한 가설에서 제시된 upper bound다).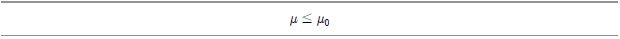
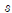 에 대해 정의하면 다음과 같다.
에 대해 정의하면 다음과 같다.
![>xbar = 2.1 #표본평균 >mu0 = 2 #가설수립에 적용된 값 > s = 0.3 #표본표분편차 > n = 35 #표본의 크기 > t = (x-bar-mu0)/(s/sqrt(n)) #t 검정통계량 >t [1] 1.9720 > alpha = .05 >t.alpha=qt(1-alpha, df=n-1) >t.alpha [1] 1.69941 #critical value](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_85.png)
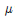 ?≤ 2라는 귀무가설을 기각한다.
?≤ 2라는 귀무가설을 기각한다.![>pval = pt (t, df=n-1, lower.tail = FALSE) >pval [1] 0.028393 #우측단측의 p값](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_86.png)
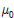 는 실제 모집단 평균?
는 실제 모집단 평균?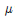 의 추정치).
의 추정치).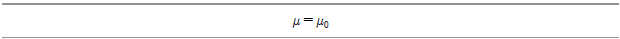
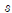 를 기준으로 정의하면 다음과 같다.
를 기준으로 정의하면 다음과 같다.
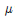 ?= 15.4).
?= 15.4).![> xbar = 14.6 > mu0 = 15.4 > s = 2.5 > n = 35 > t = (xbar-mu0)/(s/sqrt(n)) > t [1] -1.8931 > alpha = .05 > t.half.alpha = qt(1-alpha/2, df=n-1) > c (-t.half.alpha, t.half.alpha) [1] -2.0322 2.0322](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_89.png)
![> pval = 2 * pt(t, df=n-1) > pval [1] 0.066876 #양측검정의 p-value](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_90.png)
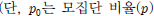 의 추정치 하한 (lower bound)이다.
의 추정치 하한 (lower bound)이다.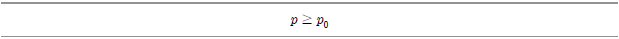
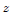 를 표본비율과 표본의 수로 정의하면 다음과 같다.
를 표본비율과 표본의 수로 정의하면 다음과 같다.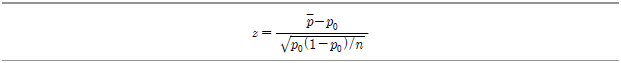
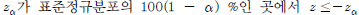 일 경우 좌측의 단측검정에 대한 귀무가설을 기각할 수 있게 된다. 예를 들어 살펴 보자. 지난 번 선거에서는 60%의 유권자가 투표에 참가하였다. 이번 선거의 경우 전화설문조사에서 148명 중 85명이 투표에 참여하였다고 응답하였다. 0.05의 유의도 수준에서 다음의 귀무가설을 기각할 수 있는지 검정하라.
일 경우 좌측의 단측검정에 대한 귀무가설을 기각할 수 있게 된다. 예를 들어 살펴 보자. 지난 번 선거에서는 60%의 유권자가 투표에 참가하였다. 이번 선거의 경우 전화설문조사에서 148명 중 85명이 투표에 참여하였다고 응답하였다. 0.05의 유의도 수준에서 다음의 귀무가설을 기각할 수 있는지 검정하라.![> xbar = 14.6 > mu0 = 15.4 > s = 2.5 > n = 35 > t = (xbar-mu0)/(s/sqrt(n)) > t [1] -1.8931 > alpha = .05 > t.half.alpha = qt(1-alpha/2, df=n-1) > c(-t.halt.alpha, t.half.alpha) [1] -2.0322 2.0322](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_95.png)
![> pval = pnorm(z) > pval [1] 0.2618 #lower tail p-value](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_96.png)


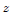 를 표본비율과 표본크기로 정의하면 다음과 같다.
를 표본비율과 표본크기로 정의하면 다음과 같다.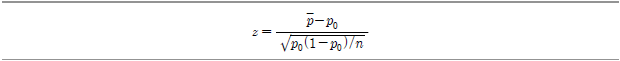
![> pbar = 30/214 > p0 = .12 > n = 214 > z = (pbar-p0)/sqrt(p0*(1-p0)/n) > z [1] 0.90875 > alpha = .05 > z.alpha = qnorm(1-alpha) > z.alpha [1] 1.6449](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_100.png)
![> pval = pnorm(z, lower.tail = FALSE) > pval [1] 0.18174 #upper tail p-value](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_101.png)

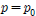 이며 표본통계량?
이며 표본통계량?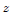 를 표본비율과 표본 크기를 기준으로 정의하면 다음과 같다.
를 표본비율과 표본 크기를 기준으로 정의하면 다음과 같다.
![> pbar = 12/20 > p0 = .5 > n = 20 > z = (pbar-p0)/sqrt(p0*(1-p0)/n) > z [1] 0.89443 > alpha = .05 > z.half.alpha.=qnorm(1-alpha/2) > c(-z.half.alpha, z.half,alpha) [1] -1.9600 1.9600](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_105.png)
![> pval = 2*pnorm(z, lower.tail = FALSE) #upper tail >pval [1] 0.37109 #양측검정의 p-value](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_106.png)




![[함수표준형] t.test(x, y = NULL, alternative = c("two.sided", "less", "greater"), mu = 0, paired = FALSE, var equal = FALSE, conf.level = 0.95, ...) [옵션 파라미터] x, y = 데이터 수치값 alternative = 대립가설에 대해 양측검정을 할 것인지 또는 단측검정을 할 것인지의 지정 mu = 표준값(또는 두 개의 표본이 있는 경우는 이들 각각 표준값의 차이) paired = 대응표본인지 여부 var.equal = 분산값을 같은 것으로 처리할지 여부 (TRUE인 경우에는 통합분산 (pooled variance)를 통해 분산을 추정한다. conf.level = 구간의 신뢰도](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_111.png)
![> mtcars$am [1] 1 1 1 0 0 0 0 0 ... > L = mtcars$am = 0 > mpg.auto = mtcars[L,]$mpg > mpg.auto #자동변속장치의 마일리지 [1] 21.4 18.7 18.1 14.3 24.4 ... By applying the negation of L, we can find the gas mileage for manual transmission. > mpg.manual = mtcars[!L,]$mpg > mpg.manual #수동변속기의 마일리지 [1] 21.0 21.0 22.8 32.4 30.4 ... We can apply the t.test function to compute the difference in means of the two sample data. > t.test(mpg.auto, mpg.manual) Welch Two Sample t-test data: mpg.auto, mpg.manual t=-3.7671, df = 18.332, p-value = 0.001374 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -11.2802 -3.2097 sample estimates: mean of x mean of y 17.147 24.392](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_112.png)




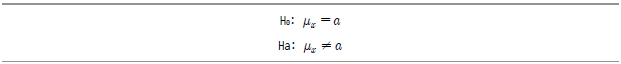
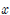 라고 가정한다. 즉, 이 경우의 p값이란 우리가 Z-score의 절대값보다 큰 (또는 Z-score의 음수값보다 작은) 표본평균을 얻을 확률을 뜻하게 된다.
라고 가정한다. 즉, 이 경우의 p값이란 우리가 Z-score의 절대값보다 큰 (또는 Z-score의 음수값보다 작은) 표본평균을 얻을 확률을 뜻하게 된다.![> a <-5 > s <-2 #표준편차 > n <-20 #표본의 크기 > xbar <-7 #표본의 평균 > z <-(xbar-a)/(s/sqrt(n)) >z [1] 4.472136 > 2*pnorm(-abs(z)) [1] 7.744216e-06](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_118.png)
![> a <-5 > s < -2 > n <-20 > xbar <-7 > 2*(1-pnorm(xbar, mean=a, sd=s/sqrt(20))) [1] 7.744216e-06](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_119.png)
![> a <-5 > s <-2 > n <-20 > xbar <-7 > t <-(xbar-a)/(s/sqrt(n)) > t [1] 4.472136 > 2*pt(-abs(t), df=n-1) [1] 0.0002611934](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_120.png)
![> w1 <-read.css(file="w1.dat", sep=",", head=TRUE) > summary(w1) Min. : 0.130 / 1st Qu. : 0.480 / Median : 0.720 / Mean : 0.765 / 3rd Qu. : 1.008 / Max. :1.760 > length(w1$vals) [1] 54](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_123.png)
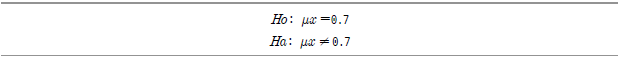
![> t <- (mean(w1$vals)-0.7)/(sd(w1$vals)/sprt(length(w1$vals))) > t [1] 1.263217 > 2*pt(-abs(t), df=length(w1$vals)-1) [1] 0.21204](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_122.png)
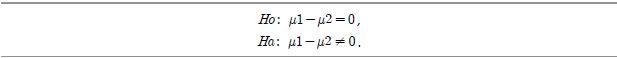
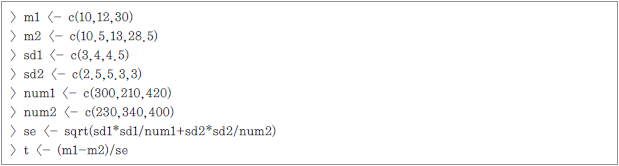
![> m1 [1] 10 12 30 > m2 [1] 10.5 13.0 28.5 > sd1](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_126.png)
![[1] 3.0 4.0 4.5 > sd1 [1] 2.5 5.3 3.0 > num1 [1] 300 210 420 > num2 [1] 230 340 400 > se [1] 0.2391107 0.3985074 0.2659216 > t [1] -2.091082 -2.509364 5.640761](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_127.png)
![>pt (t, df=pmin(num1, num2)-1) [1] 0.01881168 0.00642689 0.99999998](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_128.png)
![> pt (-abs(t), df=pmin(num1, num2)-1) [1] 1.881168e-02 6.426890e-03 1.605968e-08](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_129.png)





 ?적합성 검정
?적합성 검정 가 각각의 범주에 대한 기대값 e와 동일하다고 하는 것이다. 만약 다음의?
가 각각의 범주에 대한 기대값 e와 동일하다고 하는 것이다. 만약 다음의?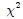 검정통계량의 p-value가 주어진 유의도 수준보다 작다면 이는 기각된다.
검정통계량의 p-value가 주어진 유의도 수준보다 작다면 이는 기각된다.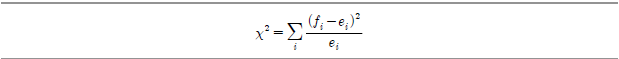
![> library(MASS) > levels(survey$Smoke) [1] "Heavy" "Never" "Occas" "Regul"](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_136.png)


![[함수 표준형] chisq.test(x, y = NULL, correct = TRUE, p=rep(1/length(x)), rescale.p=FALSE, simulate.p.value = FALSE, B=2000) [옵션 파라미터] x, y = 수치 벡터 또는 매트릭스(단, x, y는 동시에 factor 값도 가능) correct = 2x2 테이블에 대한 검정통계 계산 시 연속성수정(continuity correction)을 적용할지 여부 p=x에 대한 확률벡터 rescale.p = p값에 대해 rescale 작업을 할지 여부 simulate.p.value=p값을 계산함에 있어 Monte Carlo 시뮬레이션을 적용할지 여부 B=Monte Carlo 시뮬레이션을 적용할 때의 replicate의 개수 지정](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_139.png)
 ?독립성 검정
?독립성 검정 와?
와? 가 있을 때 한 변수의 확률분포가 다른 변수의 확률분포에 의해 영향 받지 않는다면 이들은 상호 독립적(independent )이라고 부른다.?
가 있을 때 한 변수의 확률분포가 다른 변수의 확률분포에 의해 영향 받지 않는다면 이들은 상호 독립적(independent )이라고 부른다.?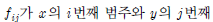 ?범주에 동시에 속하는 경우의 관측된 빈도수라고 가정한다. 또한?
?범주에 동시에 속하는 경우의 관측된 빈도수라고 가정한다. 또한?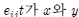 ?서로 독립적인 경우의 기대되는 count라고 가정한다. 이때 만약 다음의?
?서로 독립적인 경우의 기대되는 count라고 가정한다. 이때 만약 다음의?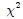 검정통계량의 p값이 주어진 유의도수준?
검정통계량의 p값이 주어진 유의도수준?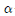 보다 작다면 독립성 가정에 대한 귀무가설은 기각된다.
보다 작다면 독립성 가정에 대한 귀무가설은 기각된다.


![> ctbl = cbind(tbl[,"Freq"], tbl[,"None"] + tbl[,"Some"]) > ctbl > chisq.test(ctbl) Pearson's Chi-squared test data: ctbl X-squared = 3.2328, df = 3, p-value = 0.3571](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_145.png)

![[그림 Ⅳ-2-2] SST (총편차제곱합)의 구성](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_147.png)


![[함수 표준형] aov(formula, data = NULL, projections = FALSE, qr = TRUE, contrasts = NULL, ...) [옵션파라미터] formula = 모델의 표현식 data = 적용 데이터 projections = projection을 반환할지 여부 qr = QR 분해를 반환할지 여부](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_150.png)

![[그림 Ⅳ-2-3] InsectSprays 데이터 세트에 대한 일위 ANOVA 분석결과](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_152.png)
![> prod_A <-c(22, 42, 44, 52, 45, 37) > prod_B <-c(52, 33, 8, 47, 43, 32) >prod_c <-c(16, 24, 19, 18, 34, 39) > revenue <- cbind(prod_A, prod_B, prod_C) > r <-c(t(as.matrix(revenue))); r # r: response data [1] 22 52 16 42 33 24 44 8 19 52 47 18 45 43 34 37 32 39 >f <-c("Prodct A", "Prodct B", "Prodct C")](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_153.png)
![> k<-3 # number of treatment level > n <-6 # observations per treatment > tm <- gl(k, 1, n*km, factor(f)); tm [1] Prodct A Prodct B Prodct C Prodct A Prodct B Prodct C Prodct A Prodct B Prodct C Prodct A Prodct B [12] Prodct C Prodct A Prodct B Prodct C Prodck A Prodct B Prodct C Prodct A Prodct B Prodct C Prodct A Prodct B [12] Prodct C Prodct A Prodct B Prodct C Prodct A Prodct B Prodct C Levels: Prodct A Prodct B Prodct C > # apply aov() to a formula that describes r by treatment factor tm > av <- aov(r~tm) > # Print out the ANOVA table with the summary function. > summary (av) Df Sum Sq Mean Sq F value Pr(>F) tm 2 745.4 372.7 2.541 0.112 Residuals 15 2200.2 146.7](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_154.png)




![[그림 Ⅳ-2-4] chocolate$Tipo의 신뢰수준 차](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_159.png)
![[그림 Ⅳ-2-5] 무선화 구획설계](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_160.png)

![[그림 Ⅳ-2-6] 무선화구획설계에서의 총제곱합의 구성요소(SST = SSC + SSR + SSE)](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_162.png)
![[그림 Ⅳ-2-7] 이위 (2-way) 요인분석](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_163.png)


![[그림 Ⅳ-2-8] 치아성장데이터의 상자도표(오른쪽 그림: 상호작용 도표)](https://dataonair.or.kr/publishing/img/dbguide/bigdata_technology/421_bigdata_166.png)



